Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
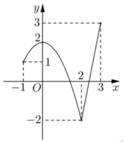
Đặt t = -sinx + 2 vì ![]() Xét hàm số y = f(t) với
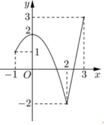
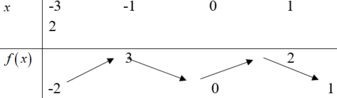
Xét hàm số y = f(t) với ![]() từ đồ thị đã cho, ta có:
từ đồ thị đã cho, ta có:
![]()
![]()

Chọn đáp án D.
Đặt t = - sin x + 2 vì - 1 ≤ sin x ≤ 1
⇒ t ∈ - 1 ; 3
Do đó
M = m a x [ - 1 ; 3 ] f t = f 3 = 3
m i n [ - 1 ; 3 ] f t = f 2 = - 2 ⇒ M - m = 5

Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 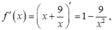
![]()
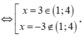
Có ![]()
![]()
Vậy m + M = 16.

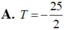

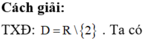
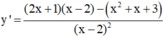
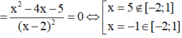
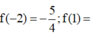
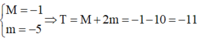

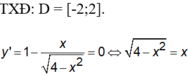
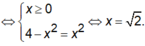
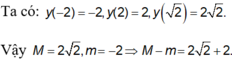

\(y=2017x+x\sqrt{2019-x^2}\)
\(y'=2017+\sqrt{2019-x^2}-\frac{x^2}{\sqrt{2019-x^2}}\)
Xét pt \(y'=0\)
Đặt \(\sqrt{2019-x^2}=t>0\Rightarrow x^2=2019-t^2\)
\(\Rightarrow2017+t-\frac{2019-t^2}{t}=0\)
\(\Leftrightarrow2t^2+2017t-2019=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{2019}{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2019-x^2}=t\Rightarrow x=\pm\sqrt{2018}\)
\(y\left(-\sqrt{2019}\right)=-2017\sqrt{2019}\) ; \(y\left(\sqrt{2019}\right)=2017\sqrt{2019}\)
\(y\left(-\sqrt{2018}\right)=-2018\sqrt{2018}\) ; \(y\left(\sqrt{2018}\right)=2018\sqrt{2018}\)
So sánh 4 giá trị trên ta thấy: \(\left\{{}\begin{matrix}M=2018\sqrt{2018}\\m=-2018\sqrt{2018}\end{matrix}\right.\)
Sao lại phải tính cả \(y\left(-\sqrt{2019}\right)\) và \(y\left(\sqrt{2019}\right)\) vậy b!