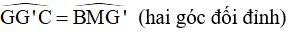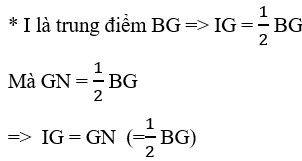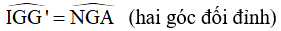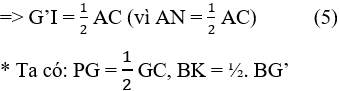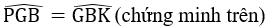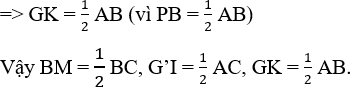Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
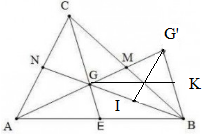
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
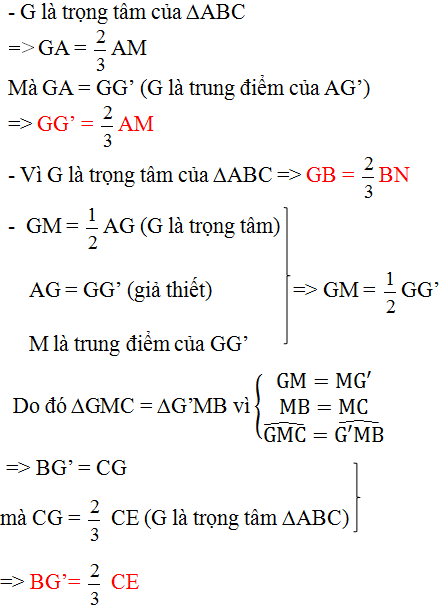
=> GA =  AM
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ =  AM
AM
Vì G là trọng tâm của ∆ABC => GB =  BN
BN
Mặt khác : GM =  AG ( G là trọng tâm )
AG ( G là trọng tâm )
AG = GG’ (gt)
GM =  GG’
GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
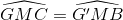
=> BG' = CG
mà CG =  CE (G là trọng tâm ∆ABC)
CE (G là trọng tâm ∆ABC)
=> BG' =  CE
CE
Vậy mỗi cạnh của ∆BGG' bằng  đường trung tuyến của ∆ABC
đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM =  BC
BC
Vì IG =  BG (I là trung điểm BG)
BG (I là trung điểm BG)
GN =  BG ( G là trọng tâm)
BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' = 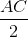
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE =  GC (G là trọng tâm ∆ABC)
GC (G là trọng tâm ∆ABC)
=> GE =  BG
BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 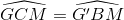 (lại góc sole trong)
(lại góc sole trong)
=> CE // BG' => 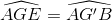 (đồng vị)
(đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE =  AB nên GK =
AB nên GK =  AB
AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
Hướng dẫn làm bài:
a)So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC
BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA=23AMGA=23AM
Mà GA = GG’ (G là trung điểm của AG’)
=> GG′=23AMGG′=23AM
Vì G là trọng tâm của ∆ABC => GB=23BNGB=23BN
Mặt khác :
M là trung điểm GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′
Do đó ∆GMC=∆G’MB vì ⎧⎪⎨⎪⎩GM=MG′MB=MCˆGMC=ˆG′MB{GM=MG′MB=MCGMC^=G′MB^
=> BG′=CGCG=23CEBG′=CGCG=23CE (G là trọng tâm tam giác ABC)
=>BG′=23CE=>BG′=23CE
Vậy mỗi cạnh của ∆BGG’ bằng 2323 đường trung tuyến của ∆ABC
b)So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC.
-Ta có: BM là đường trung tuyến ∆BGG’
Mà M là trung điểm của BC nên BM=12BCBM=12BC
Vì IG=12BGIG=12BG (Vì I là trung điểm BG)
GN=12BGGN=12BG (G là trọng tâm)
=> IG = GN
Do đó ∆IGG’=∆NGA (c.g.c) => IG′=AN=>IG′=AC2IG′=AN=>IG′=AC2
-Gọi K là trung điểm BG => GK là trung điểm ∆BGG’
Vì GE=12GCGE=12GC (G là trọng tâm tam giác ABC)
BG' = GC (Chứng minh trên)
=>GE=12BG=>GE=12BG
Mà K là trung điểm BG’ =>KG’ = EG
Vì ∆GMC = ∆G’MB (chứng minh trên)
=> ˆGCM=ˆG′BMGCM^=G′BM^ (So le trong)
=>CE // BG’ => ˆAGE=ˆAG′BAGE^=AG′B^ (đồng vị)
Do đó ∆AGE = ∆GG’K (c.g.c) =>AE = GK
Mà AE=12AB⇒GK=12AB

Bài giải
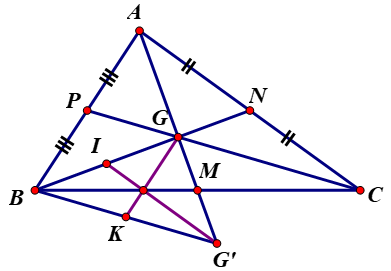
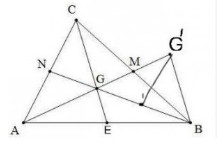
a) Gọi M, N, E lần lượt là trung điểm của AB, BC, CA.
Vậy mỗi cạnh của ΔBGG' bằng 2/3 đường trung tuyến của ΔABC.
b) Gọi I, K lần lượt là trung điểm của BG và BG'.


gọi tam giác ABC có các đường trung tuyến là AI, BH, CF
a, nhận xét: ta thấy tam giác BGG' có các cạnh =2/3 các trung tuyến của tam giác ABC theo các cặp tương ứng
BG=2/3BH , BG'=2/3CF , GG'=2/3AI
chưng minh:
ta có :
*BG=2/3BH theo tính chất đường trung tuyến
* xét tứ giác BGCG' có
- I là trung điểm của BC ( theo giả thiết)
- I là trung điểm của GG'
VÌ: GG'=AG
GI=1/2AG
=> GI =1/2GG'
=> I là trung điểm của GG'
=>tứ giác BGCG' là hình thoi
=>BG'=GC
=>BG'=2/3CF
*như chứng minh trên ta có
AG=GG'
mà AG=2/3AI
=> GG'=2/3AI
=> ĐIỀU CẦN CHỨNG MINH
b,gọi các điểm J,K lằn lượt là trung điểm của BG, BG'
nhận xét; ta thấy các đường trung tuyến của BGG'=1/2 các cạnh của ABC tương ứng
*BI=1/2BC( gia thuyết)
*cm:GK=1/2AB
xét tam gác ABG'
G là trung điểm của AG'
K là trung điểm của BG'
=> GK=1/2AB (tính chất đường trung tuyến)
*cm; G'J=1/2AC
GH=1/2BG
JG=1/2BG
=>GH=JG
GA=GG'(giả thuyết)
=> tứ giác AJG'H là hình thoi
=> JG'=AH
AH=1/2AC
=>JG'=1/2AC
điều phải chứng minh
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC:
gọi M;N;P là trung điểm của BC; AC; AB
cạnh của tam giác BGG" là:
BG = 2/3.BN
GG' = AG = 2/3.AM
BG' =- CG = 2/3.CP ( do tam giác BG'M = CMG => BG'=CG)
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC:
Gọi I là trung điểm GG', K là trung điểm BG
BM = BC/2
GI = AB/2 ( AG là đường trung bình của tam giác BGG')
G'K = AN = AC/2 ( tg ANG= tgG'GK => G'K= AN)

a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC.
Gọi M, N, E lần lượt là trung điểm của BC, CA, AB.
- G là trọng tâm của ∆ABC
⇒⇒ GA = \(\frac{2}{3}\) AM
Mà GA = GG’ (G là trung điểm của AG’)
⇒⇒ GG' = \(\frac{2}{3}\) AM
- Vì G là trọng tâm của ∆ABC ⇒⇒ GB = \(\frac{2}{3}\) BN
- Ta có:
GM = \(\frac{1}{2}\) AG (do G là trọng tâm) và AG = GG' (gt)
⇒⇒ GM = \(\frac{1}{2}\) GG'
Xét ∆GMC và ∆G’MB có:
GM = MG'
MB = MC
ˆGMC=ˆG′MBGMC^=G′MB^ (hai góc đối đỉnh)
Vậy ∆GMC=∆G’MB.
⇒⇒ BG' = CG
Mà CG = \(\frac{2}{3}\) CE (G là trọng tâm tam giác ABC)
⇒⇒ BG' = \(\frac{2}{3}\) CE
Vậy mỗi cạnh của ∆BGG’ bằng \(\frac{2}{3}\) đường trung tuyến của ∆ABC.
b) So sánh các đường trung tuyến của ∆BGG’ với các cạnh của ∆ABC.
- Ta có: BM là đường trung tuyến ∆BGG’
Mà M là trung điểm của BC nên BM = \(\frac{1}{2}\) BC
Vì IG = \(\frac{1}{2}\) BG (Do I là trung điểm BG)
GN = \(\frac{1}{2}\) BG (G là trọng tâm)
⇒⇒ IG = GN
Xét ∆IGG’ và ∆NGA có:
IG = GN (cmt)
GG' = GA (gt)
ˆIGG′=ˆNGAIGG′^=NGA^ (hai góc đối đỉnh)
Vậy ∆IGG’ = ∆NGA (c.g.c) ⇒ IG' = AN ⇒ IG' = AC2AC2
- Gọi K là trung điểm BG ⇒ GK là trung tuyến của ∆BGG’
Vì GE = \(\frac{1}{2}\) GC (G là trọng tâm tam giác ABC)
BG' = GC (cmt)
⇒⇒ GE =\(\frac{1}{2}\) BG'
Mà K là trung điểm BG’ ⇒⇒ KG’ = EG
Vì ∆GMC = ∆G’MB (cmt)
⇒⇒ ˆGCM=ˆG′BMGCM^=G′BM^ (hai góc tương ứng)
⇒⇒ CE // BG’ ⇒ ˆAGE=ˆAG′BAGE^=AG′B^ (đồng vị)
Xét ∆AGE và ∆GG’K có:
EG = KG’ (cmt)
AG = GG' (gt)
ˆAGE=ˆAG′BAGE^=AG′B^ (cmt)
Vậy ∆AGE = ∆GG’K (c.g.c) ⇒⇒ AE = GK
Mà AE = \(\frac{1}{2}\) AB ⇒⇒ GK = \(\frac{1}{2}\) AB
Vậy mỗi đường trung tuyến của ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó

A B C G' G P M N
a) Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC
Theo tính chất đường trung tuyến của tam giác ta có:
GB = 2/3.BN (1)
GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)
GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = GM’ .
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
MC = MB
⇒ ΔGMC = ΔG’MB (c.g.c)
⇒ GC = G’B (hai cạnh tương ứng).
Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)
Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.
A B C M G' P N K G I
b) Gọi I, K lần lượt là trung điểm của BG, BG’.
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)
Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)