
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân số liên tục (Liên phân số) còn gọi là liên phân số là một dạng biểu diễn các số thực dương, cả hữu tỷ và vô tỷ, dưới dạng một phân số nhiều tầng.
VD : \(\frac{9}{7}=1+\frac{1}{3+\frac{1}{2}}\)
Chúc bạn học tốt!

Tỉ lệ xích là 1:125 nên 1cm trên bản đồ ứng với 125cm trên thực tế
Suy ra chiều dài thật của máy bay là: 56,408.125= 7051cm = 70,51m
Giải:
Chiều dài thật của chiếc máy bay Bô-inh( Boeing) là:
56,408 . 125 = 7051(cm)
Đổi: 7051cm = 70,51m
Đáp số: 70,51 m

Olm sẽ hướng dẫn các em phương pháo giải tổng quát dạng này như sau:
Bước 1 phân tích số đã cho thành tích của các số nguyên tố
Bước 2 nhóm các thừa số nguyên tố thành 1 nhóm ta sẽ được tích của hai số cần tìm
2499 = 3 \(\times\) 7 \(\times\) 7 \(\times\) 17
2499 = ( 7 \(\times\) 7) \(\times\) ( 3 \(\times\) 17)
2499 = 49 \(\times\) 51

Đáp án B.
Do bạn Hà đã bấm một số có 6 chữ số nhưng chỉ có số 2007 xuất hiện trên màn hình nên trong số mà bạn Hà có thể nhập có 2 chữ số 1.
Có hai trường hợp xảy ra.
TH1: Hai chữ số 1 không đứng cạnh nhau.
TH2: Hai chữ số 1 đứng cạnh nhau.
Giải quyết:
TH1: Xếp 4 chữ số 2; 0; 0; 7 có 1 cách.
Giữa các chữ số 2; 0; 0; 7 tạo ra được 5 vách ngăn. Xếp 2 chữ số 1 vào 5 vách ngăn có C 5 2 = 10 cách => có 10 số có thể tạo thành ở TH1.
TH2: Xếp 4 chữ số 2; 0; 0; 7 có 1 cách.
Buộc hai chữ số 1; 1 vào nhau được 1 cách.
Xếp cặp số 11 vào 5 vách ngăn có 5 cách =>có 5 số có thể tạo thành ở TH2.
Vậy có tất cả 10 + 5 = 15 số mà bạn Hà có thể đã nhập vào máy tính. Ta chọn B.

Phương pháp chung:
Dạng: ax^n + bx^(n-1) +cx^(n-2) + dx^(n-3) +...+ z = 0
Tim nghiệm nguyên bằng cách nhẩm một nghiệm nào đó thỏa phương trình, giả sử là x0.
Hệ số theo thứ tự bậc cao về thấp:
a b c d ... z.
Nghiệm nguyên x0: a a' b' c' ... 0.
Trong đó:
+ a là hệ số được hạ xuống.
+ a' = x0*a + b.
+ b' = x0*a' + c.
+ c' = x0*b' + d.
.... đến số cuối cùng thì kết quả bằng 0.
Ta dược phương trình mới giảm đi một bậc: (x-x0)(ax^(n-1) + a'x^(n-2) + b'x^(n-3) + c'x^(n-4) +...+ 0) = 0.
Sau đó ta giải phương trình tích: <=> x=x0 hoặc ax^(n-1) + a'x^(n-2) + b'x^(n-3) +...+ 0 = 0 (*).
Nếu (*) là phương trình bậc cao hơn bậc 3 thì ta cứ thao tác như trên để đưa về phương trình tích mà phương trình cuối cùng trong phương trình tích là phương trình bậc 3 hoặc thấp hơn mà ta có thể sữ dụng máy tính để tìm nghiệm.
Quy tắc ghi nhớ:"NHÂN NGANG CỘNG CHÉO"


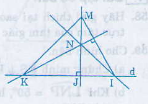
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK
bấm vào fx ý chọn thôi
quá rễ dùng ''/'' hoặc ấn fx