K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Thông cảm mk bị cận!
SG
7
DN
20 tháng 4 2017
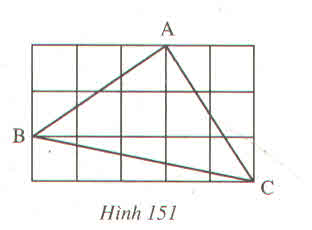
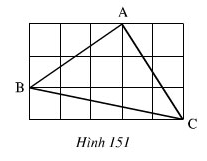
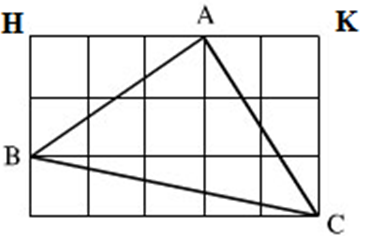
Xét tam giác ABC trên hình vẽ ta có:
AB = AC = 6 ô vuông (với điều kiện tất cả ô vuông đều bằng nhau).
=> Tam giác ABC là tam giác cân và cân tại A.
LS
0
20 tháng 10 2017
BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé
TM
20 tháng 10 2017
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)
Bài 3:
a: Xét ΔOCA và ΔOCB có
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
OA=OB
Do đó: ΔOCA=ΔOCB
b: Xét ΔOHA và ΔOHB có
OA=OB
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(1)
Ta có: CB=CA
nên C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
hay OC\(\perp\)AB
Bài 1:
a: Xét ΔCAB và ΔCDE có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔCAB=ΔCDE
b: Ta có: ΔCAB=ΔCDE
nên \(\widehat{CAB}=\widehat{CDE}\)
mà \(\widehat{CAB}=80^0\)
nên \(\widehat{CDE}=80^0\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DE