Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

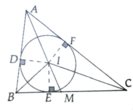
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

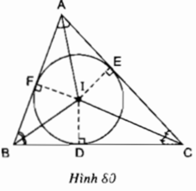
Gọi M,N,IM,N,I lần lượt là trung điểm AB,AC,ADAB,AC,AD
có M,N,IM,N,I thẳng hàng
AIEMAIEM nội tiếp⇒ˆAEF=ˆAMN⇒AEF^=AMN^(1)
AINFAINF nội tiếp ⇒ˆAFE=ˆANM⇒AFE^=ANM^(2)
(1,2)⇒ˆEDF=ˆEAF=90∘=ˆEOF⇒EDF^=EAF^=90∘=EOF^
⇒A,O,D,E,F⇒A,O,D,E,F cùng thuộc 1 đường tròn
b)
có △AEF△AEF luôn đồng dạng với △AMN△AMN cố định
⇒SAEF⇒SAEFmin khi AEAE min
có AE≥AMAE≥AM
⇒SAEF⇒SAEF min khi E≡M,F≡NE≡M,F≡N
lúc đó SAEF=bc8SAEF=bc8

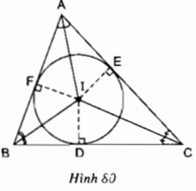
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b
A B C S1 S2 S3 D E F x c-x y a-y z b-z
Kí hiệu như trên hình vẽ.
Giả sử ngược lại, trong ba tam giác S1,S2,S3 không có tam giác nào có diện tích nhỏ hơn hoặc bằng 1/4 diện tích tam giác ABC.
Khi đó ta có : \(\frac{S_1.S_2.S_3}{S}>\frac{1}{64}\)
Hay : \(\frac{x\left(b-z\right).y\left(c-x\right).z\left(a-y\right)}{a^2b^2c^2}>\frac{1}{64}\) (*)
Mặt khác, ta có : \(x\left(c-x\right)\le\frac{\left(x+c-x\right)^2}{4}=\frac{c^2}{4}\)
Tương tự \(y\left(a-y\right)\le\frac{a^2}{4}\) , \(z\left(b-z\right)\le\frac{b^2}{4}\)
Nhân theo vế : \(x\left(c-x\right).y\left(a-y\right).z\left(b-z\right)\le\frac{a^2b^2c^2}{64}\)
hay \(\frac{x\left(b-z\right).y\left(c-x\right).z\left(a-y\right)}{a^2b^2c^2}\le\frac{1}{64}\) (vô lí - trái với (*))
Vậy giả thiết thiết phản chứng sai. Ta có đpcm.