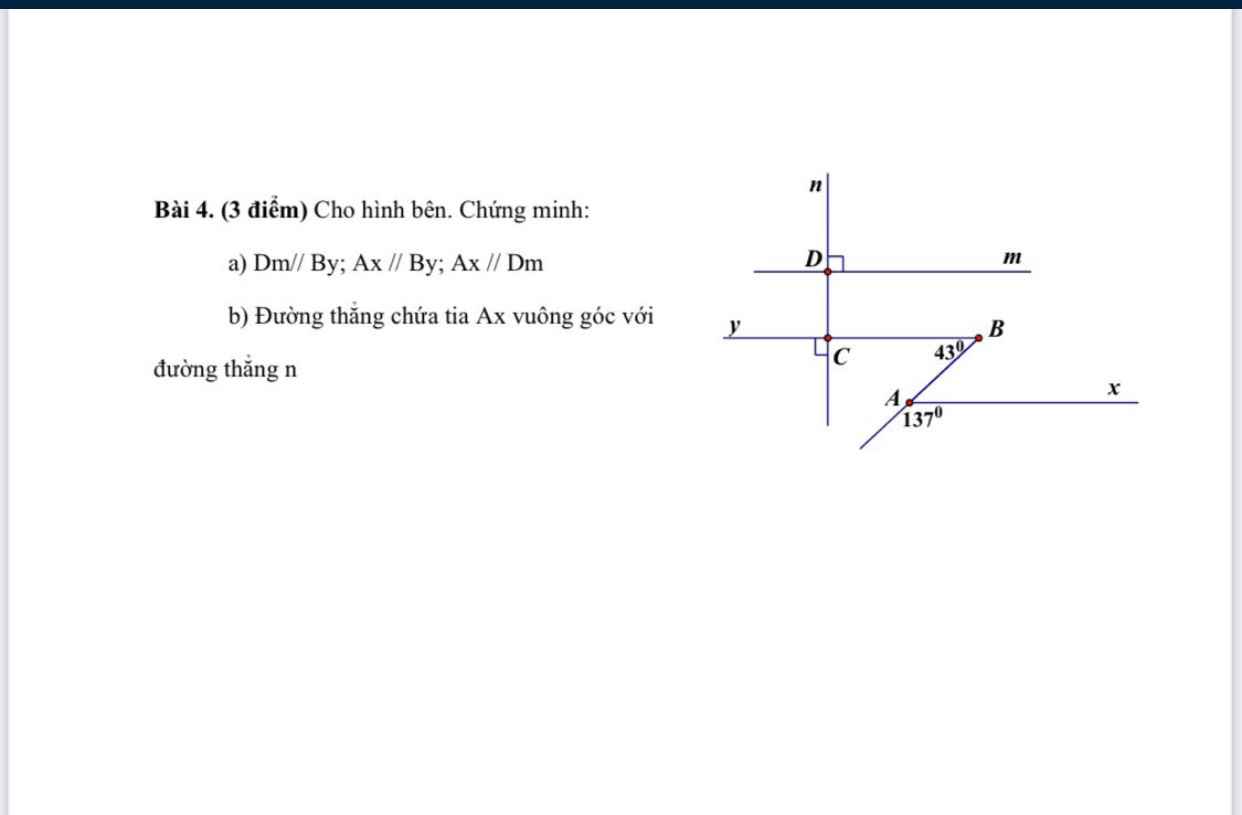
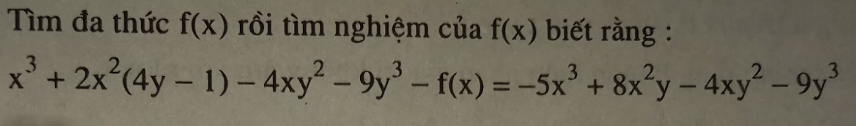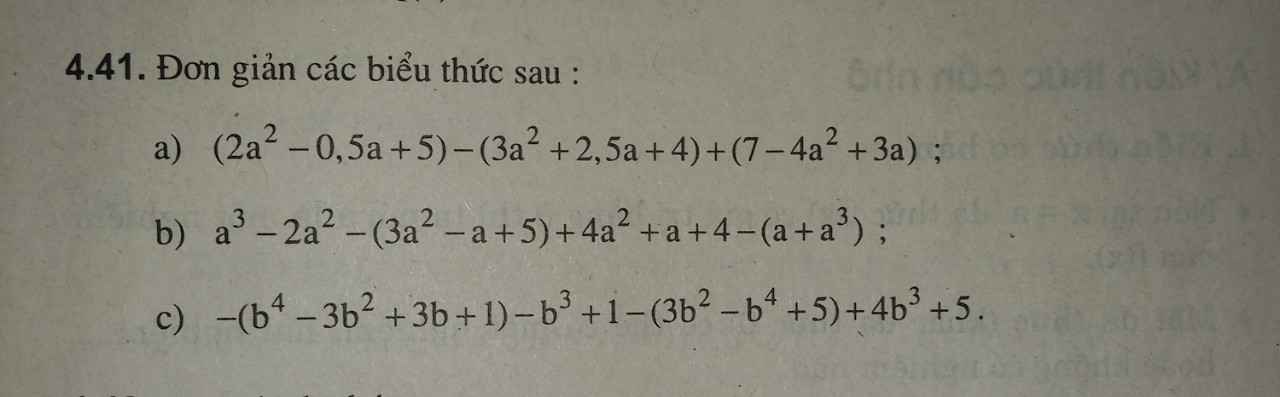Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: \(\widehat{HAD}+\widehat{BDA}=90^0\)
\(\widehat{CAD}+\widehat{BAD}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{HAD}=\widehat{CAD}\)
hay AD là tia phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó:ΔADH=ΔADK
Suy ra: AH=AK

\(x^3+2x^2\left(4y-1\right)-4xy^2-9y^3-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow\left(x^3+8x^2y+2x^2-4xy^2-9y^3\right)-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow f\left(x\right)=x^3+8x^2y+2x^2-4xy^2-9y^3+5x^3-8x^2y+4xy^2+9y^3\\ \Rightarrow f\left(x\right)=6x^3+2x^2\)

a: \(=\left(2a^2-3a^2-4a^2\right)+\left(-0.5a-2.5a+3a\right)+\left(5-4+7\right)=-5a^2+8\)
b: \(=\left(a^3-a^3\right)+\left(-2a^2-3a^2+4a^2\right)+\left(a+a-a\right)+\left(-5+4\right)=-a^2+a-1\)
c: \(=-b^4+3b^2-3b-1-b^3+1-3b^2+b^4-5+4b^3+5\)
\(=3b^3-3b\)


1) \(\left(\dfrac{-13}{17}-\dfrac{31}{52}\right)-\left(\dfrac{73}{52}-\dfrac{13}{17}+\dfrac{5}{6}\right)-\dfrac{3}{4}\)
\(=\dfrac{-13}{17}-\dfrac{31}{52}-\dfrac{73}{52}+\dfrac{13}{17}-\dfrac{5}{6}-\dfrac{3}{4}\)
\(=\left(\dfrac{-13}{17}+\dfrac{13}{17}\right)-\left(\dfrac{31}{52}+\dfrac{73}{52}\right)-\left(\dfrac{5}{6}+\dfrac{3}{4}\right)\)
\(=0-2-\dfrac{19}{12}\)
\(=-2-\dfrac{19}{12}\)
\(=\dfrac{-43}{12}\)



\(b,\sqrt{36}.\sqrt{\dfrac{25}{26}}+\dfrac{1}{4}\\ =\sqrt{6^2}.\sqrt{\left(\dfrac{5}{4}\right)^2}+\dfrac{1}{4}\\=6.\dfrac{5}{4}+\dfrac{1}{4}=\dfrac{30}{4}+\dfrac{1}{4}=\dfrac{31}{4}\)
\(c,\sqrt{\dfrac{4}{81}}:\sqrt{\dfrac{25}{81}}-1\dfrac{2}{5}\\ =\sqrt{\left(\dfrac{2}{9}\right)^2}:\sqrt{\left(\dfrac{5}{9}\right)^2}-\dfrac{7}{5}\\ =\dfrac{2}{9}:\dfrac{5}{9}-\dfrac{7}{5}\\ =\dfrac{2}{9}.\dfrac{9}{5}-\dfrac{7}{5}=\dfrac{2}{5}-\dfrac{7}{5}\\ =-1\)
\(d, 0,1.\sqrt{225}.\sqrt{\dfrac{1}{4}}\\ =\dfrac{1}{10}.\sqrt{15^2}.\sqrt{\left(\dfrac{1}{2}\right)^2}\\ =\dfrac{1}{10}.15.\dfrac{1}{2}=\dfrac{3}{5}\)
\(e, \dfrac{3^{25}}{9^3.3^{16}}\\ =\dfrac{3^{25}}{\left(3^2\right)^3.3^{16}}\\ =\dfrac{3^{25}}{3^6.3^{16}}\\ =\dfrac{3^{25}}{3^{22}}\\ =3^3=27\)