
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500

2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499


Trả lời:
\(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{\left(5x+1\right)\left(5x+6\right)}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5x+1}-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=1-\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=\frac{1}{2006}\)
\(\Rightarrow5x+6=2006\)
\(\Rightarrow5x=2000\)
\(\Rightarrow x=400\)
Vậy x = 400
Trả lời:
\(\frac{x}{2008}-\frac{1}{10}-\frac{1}{15}-\frac{1}{21}-...-\frac{1}{120}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}-\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\right)=\frac{5}{8}\)\(\frac{5}{8}\)
Đặt \(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\), ta được : \(\frac{x}{2008}-A=\frac{5}{8}\) (*)
\(\Rightarrow A=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(\Rightarrow A=2\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{240}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{16}\right)=2.\frac{3}{16}=\frac{3}{8}\)
Thay A vào (*) , ta có:
\(\frac{x}{2008}-\frac{3}{8}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}=1\)
\(\Rightarrow x=2008\)
Vậy x = 2008

\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)



mọi người ơi, đây có phải là đáp án đúng của bài 1 không ạ, nếu đúng thì giúp em viết ra giống như trên với ạ, em nhìn được nhưng 1 số chỗ không rõ lắm, huhu

Bài 5:
30 phút = \(\dfrac{1}{2}\) giờ
Thời gian gia đình bạn Tuấn đi từ Hà Nội tới Phan Thiết tới là:
\(\dfrac{13}{4}\) + \(\dfrac{1}{2}\) + \(\dfrac{13}{3}\) = \(\dfrac{97}{12}\) giờ
\(\dfrac{95}{12}\) giờ = 8 giờ 5 phút
b; Gia đình bạn Tuấn đến thành Phố Phan Thiết lúc:
6 giờ + 8 giờ 5 phút = 14 giờ 5 phút
Kl...
Bài 6:
a; -3 - \(\dfrac{2}{5}\) ≤ \(x\) ≤ \(\dfrac{1}{2}\) - \(\dfrac{-3}{4}\)
- \(\dfrac{17}{5}\) ≤ \(x\) ≤ \(\dfrac{5}{4}\)
-3,4 ≤ \(x\) ≤ 1,25
Vì \(x\) là số nguyên nên \(x\) \(\in\) {-3; -2; -1; 0; 1}
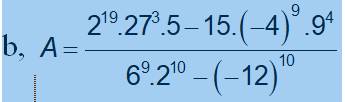


 Mình cảm ơn ạ
Mình cảm ơn ạ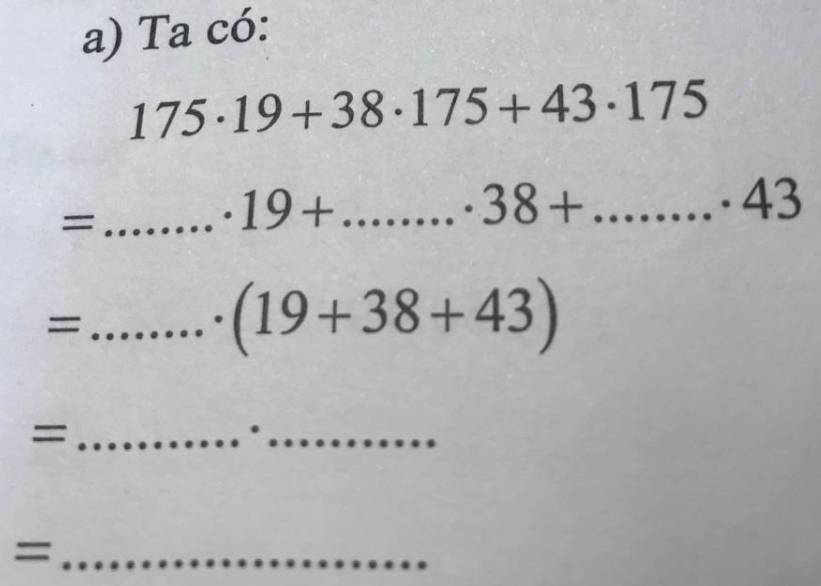
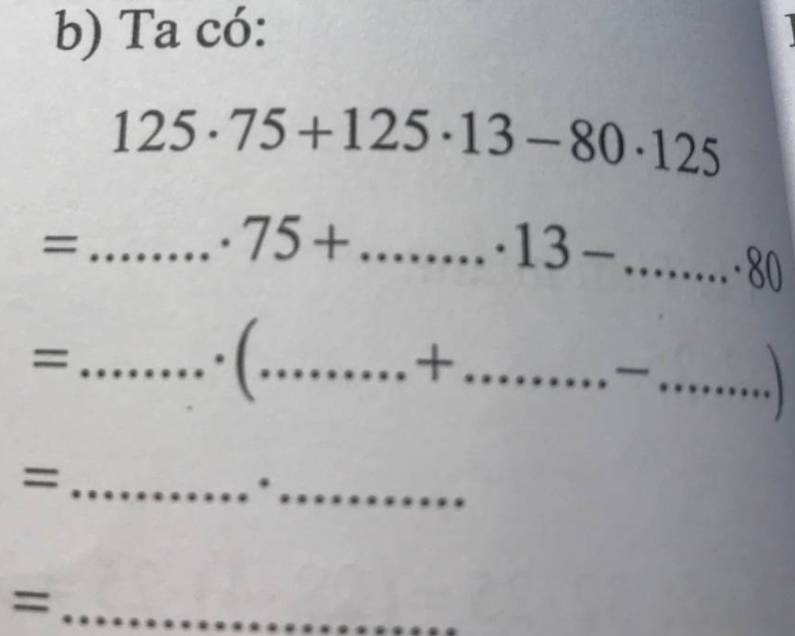
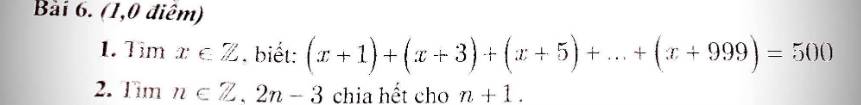
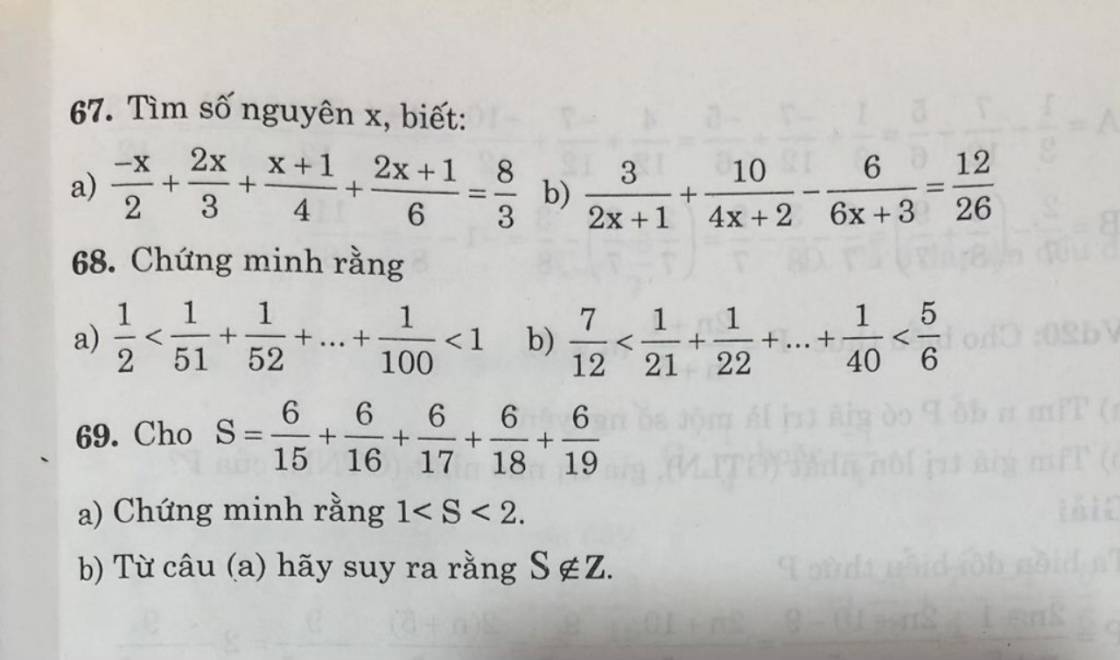


 MÌNH ĐANG CẦN GẤP LÀM NHANH GIÚP MÌNH VỚI Ạ:))
MÌNH ĐANG CẦN GẤP LÀM NHANH GIÚP MÌNH VỚI Ạ:))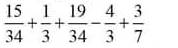



\(=\dfrac{2^{19}\cdot3^9\cdot5+2^{18}\cdot3^9\cdot5}{2^{19}\cdot3^9-2^{20}\cdot3^{10}}\)
\(=\dfrac{2^{18}\cdot3^9\cdot5\left(2+1\right)}{2^{19}\cdot3^9\left(1-2\cdot3\right)}=\dfrac{1}{2}\cdot\dfrac{5\cdot3}{-5}=-\dfrac{3}{2}\)
\(A=\dfrac{2^{19}\cdot27^3\cdot5-15\cdot\left(-4\right)^9\cdot9^4}{6^9\cdot2^{10}-\left(-12\right)^{10}}\)
\(A=\dfrac{2^{19}\cdot\left(3^3\right)^3\cdot5-3\cdot5\cdot-\left(2^2\right)^9\cdot\left(3^2\right)^4}{2^9\cdot3^9\cdot2^{10}-\left(2^2\right)^{10}\cdot3^{10}}\)
\(A=\dfrac{2^{19}\cdot3^9\cdot5+3^9\cdot2^{18}\cdot5}{2^{19}\cdot3^9-2^{20}\cdot3^{10}}\)
\(A=\dfrac{2^{18}\cdot3^9\cdot5\cdot\left(2+1\right)}{2^{19}\cdot3^9\cdot\left(1-2\cdot3\right)}\)
\(A=\dfrac{1\cdot1\cdot5\cdot3}{2\cdot1\cdot-5}\)
\(A=-\dfrac{1}{2}\cdot3\)
\(A=-\dfrac{3}{2}\)