Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lấy A(2;0), B(0;2) thuộc d, Ta có ảnh của A và B qua phép quay tâm O góc \(90^o\) lần lượt là B=(0;2) và A' = (-2;0). Do đó ảnh của d qua phép quay tâm O góc \(90^o\) là đường thẳng BA' có phương trình x - y + 2 = 0.

Lấy A(2;0), B(0;2) thuộc d, Ta có ảnh của A và B qua phép quay tâm O góc \(90^o\) lần lượt là B=(0;2) và A' = (-2;0). Do đó ảnh của d qua phép quay tâm O góc \(90^o\) là đường thẳng BA' có phương trình x - y + 2 = 0.

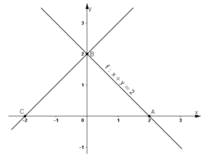
* Ta có A(2; 0) thuộc tia Ox.
Gọi Q(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).
* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.
+ A(2 ; 0) ∈ (d)
⇒ B = Q(O,90º) (A) ∈ (d’)
+ B(0 ; 2) ∈ (d).
⇒ C = Q(O,90º) (B) ∈ (d’).
Dễ dàng nhận thấy C(-2; 0) (hình vẽ).
⇒ (d’) chính là đường thẳng BC.
Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là:
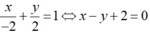

Đường tròn có pt:
\(\left(x-1\right)^2+\left(y-1\right)^2=8\)
Tâm \(I\left(1;1\right)\) và \(R=2\sqrt{2}\)
Gọi \(I_1\) là ảnh của I qua phép quay
\(\Rightarrow\left\{{}\begin{matrix}x_{I1}=1.cos\left(-45^0\right)-1sin\left(-45^0\right)=\sqrt{2}\\y_{I_1}=1.sin\left(-45^0\right)+1.cos\left(-45^0\right)=0\end{matrix}\right.\)
\(\Rightarrow I_1\left(\sqrt{2};0\right)\)
Gọi \(I_2\) là ảnh của \(I_1\) qua phép vị tự:
\(\Rightarrow\left\{{}\begin{matrix}x_{I_2}=-\sqrt{2}.\sqrt{2}=-2\\y_{I_2}=-\sqrt{2}.0=0\end{matrix}\right.\) \(\Rightarrow I_2\left(-2;0\right)\)
\(R_2=\left|-\sqrt{2}\right|.2\sqrt{2}=4\)
Vậy pt đường tròn ảnh có dạng:
\(\left(x+2\right)^2+y^2=16\)