Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tu ke hinh :
a, xet tamgiac MHB va tamgiac MKC co : HM = MK (gt)
CM = MB do M la trung diem cua BC(gt)
goc HMB = goc KMC (doi dinh)
=> tamgiac MHB = tamgiac MKC (c - g - c)
xet tamgiac HMC va tamgiac KMB co : HM = MK (gt)
goc HMC = goc KMB (doi dinh)
MC = MB (cmt)
=> tamgiac HMC = tamgiac KMB (c - g - c)
=> goc CHM = goc MKB
ma goc CHM = 90 do MH | AC (gt)
=> goc MKB = 90
b, MH | AC (gt)
tamgiac ABC vuong tai A (gt) => AB | AC (dn)
2 duong thang nay phan biet
=> HK // AB (dl)
MH | AB (gt)
goc MKB = 90 (cau a) => MK | KB
2 duong thang nay phan biet
=> AC // KB (dl)
goc AHB so le trong HBK
=> goc AHB = goc HBK (tc)
xet tamgiac AHB va tamgiac KBH co : HB chung
goc HAB = 90 = goc HKB do. ...
=> tamgiac AHB = tamgiac KBH (ch - gn)
=> AH = KB (dn)
c, tamgiac HMC = tamgiac KMB (Cau a) => CH = KB
AH = KB (Cau b)
=> CH = HA
xet tamgiacHMC va tamgiac HMA co : HM chung
goc CHM = goc MHA do HM | AC (gt)
=> tamgiacHMC = tamgiac HMA (2cgv)
=> MC = MA (dn)
=> tamgiac MCA can tai M (dn)
a) xét tam giác MHC và tam giác HKB có
MK=MH (GT)
BM=MC(GT)
GÓC M1=GÓC M2 (đối đỉnh)
suy ra tam giác MHC bằng tam giác HKB (c-g-c)
do tam giác MHC bằng tam giác HKB nên góc H bằng góc K= 90 độ
suy ra góc HKB bằng 90độ

ABC cân nên đpg Ah cx là đườg cao;AH=BC/2
=>BC=3căn2
ta có: AB*AC=BC*AH<=>AB^2=3căn2*3căn2/2<=>AB=3

a, Xét tam giác DEM và tam giác DFM có :
DE = DF ( vì tam giác DEF cân tại D )
^EDM = ^FDM ( gt )
Cạnh DM chung
Suy ra : Tam giác DEM = Tam giác DFM ( c.g.c )
Suy ra :^DME = ^DMF (1)
Mà ^DME+^DMF = 180 độ (2)
Từ (1 ) và (2) suy ra : ^DME =^DMF=180độ chia 2 =90 độ
Vậy ^DME = ^DMF = 90 độ
- Cho tam giác ABC, có AH đường cao, AD phân giác, có góc B trừ góc C=30 độ hỏi góc HAD bằng bao nhiêu


Tự vẽ hình
a) Tớ sửa đề xíu nha Tam giác ABM= tam giác CAM
Xét ...... ( tự làm )
=) Tam giác ABM= tam giác CBM ( c - c - c )
b)
sai đề
c)

- vẽ MH và MK lần lượt vuông góc với AB và AC
- Xét \(\Delta AHM\)vuông tại H và\(\Delta AKM\)vuông tại K có: AM: cạnh chung
\(\widehat{HAM}=\widehat{KAM}\)(vì AM là tia phân giác của \(\widehat{A}\))
\(\Rightarrow\)\(\Delta AHM=\Delta AKM\)(cạnh huyền - góc nhọn)
\(\Rightarrow\)MH = MK (2 cạnh tương ứng)
- Xét \(\Delta BHM\)vuông tại H và\(\Delta CKM\)vuông tại K có: BM = CM ( M là trung diểm của BC)
HM = KM (cmt)
\(\Rightarrow\)\(\Delta BHM=\Delta CKM\)(cạnh huyền - cạnh góc vuông)
\(\Rightarrow\)\(\widehat{B}=\widehat{C}\)(2 góc tương ứng)
Vậy \(\Delta ABC\)cân tại A ( vì có góc B và góc C là 2 góc ở đáy bằng nhau )
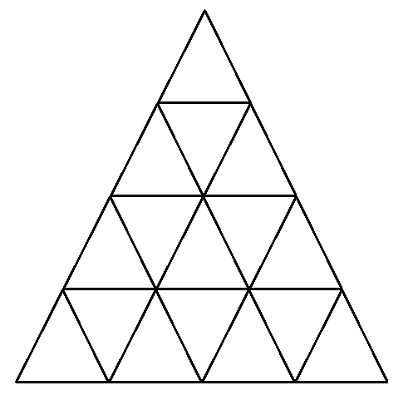
Theo như ảnh thì b học toán MTCT nên đầu tiên ta tìm ra quy luật rồi chỉ việc bấm máy!!!
Ta có: Với độ cao là 1 => số tam giác là: 1
Với độ cao là 2 => số tam giác là: (1+3)+1
Với độ cao là 3 => số tam giác là: (1+3+5)+(1+2)+1
Với độ cao là 4 => số tam giác là: (1+3+5+7)+(1+2+3)+(1+2)+1
Với độ cao là 5 => số tam giác là: (1+3+5+7+9)+(1+2+3+4)+(1+2+3)+(1+2)+1
Từ đây có thể suy ra quy luật => với độ cao là 244 thì số tam giác là:
(1+3+...+487)+(1+2+...+243)+(1+2+...+242)+...+(1+2)+1=(487+1)∗2442+244∗2432+243∗2422+...+3∗22+2∗12(487+1)∗2442+244∗2432+243∗2422+...+3∗22+2∗12
=59536+243∑1x(x+1)2∑1243x(x+1)2
=59536+2421090
=2480626
Bài viết đã được chỉnh sửa nội dung bởi Sergio BusBu: 21-12-2015 - 17:46Kira Tatsuya yêu thích