K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 3 2022
\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)
LA
9 tháng 4 2023
c/Theo công thức pascal trong Nhị Thức Newton ta có: \(C_{n-1}^{n-1}\) + \(C_{n-1}^k\) = \(C_n^k\)
C = \(C_{19}^0\) + \(C_{19}^1\) + \(C_{19}^2\) + ....+ \(C_{19}^{18}\) + \(C_{19}^{19}\)
C = (1+1)19 = 524288
còn câu d hình như đề sai
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
Phương trình đường tròn (C):
\(\left(x-1\right)^2+\left(y-2\right)^2=3^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2=9\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
Đường tròn (C) viết lại: \(\left(x-0\right)^2+\left(y-0\right)^2=3^2\)
Do đó đường tròn có tâm \(I\left(0;0\right)\) và bán kính \(R=3\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
\(\left(x-1\right)^2+\left(y+2\right)^2=25\)
\(\Leftrightarrow x^2-2x+1+y^2+4y+4=25\)
\(\Leftrightarrow x^2+y^2-2x+4y-20=0\)
5 tháng 11 2021
Bài 6:
b: PTHĐGĐ là:
\(x^2+4x-1=x-3\)
\(\Leftrightarrow x^2+3x-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=-7\\y=-2\end{matrix}\right.\)
25 tháng 11 2023
a: \(\overrightarrow{MA}=-3\cdot\overrightarrow{MB}\)
\(\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
=>\(-3\cdot\overrightarrow{MB}-\overrightarrow{MB}=\overrightarrow{BA}\)
=>\(\overrightarrow{BA}=-4\overrightarrow{MB}=4\overrightarrow{BM}\)
=>M nằm giữa A và B sao cho BA=4BM
b:
Gọi E là trung điểm của AB
Vì E là trung điểm của AB nên \(\overrightarrow{NA}+\overrightarrow{NB}=2\cdot\overrightarrow{NE}\)
\(\overrightarrow{NA}+\overrightarrow{NB}+2\cdot\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\cdot\overrightarrow{NE}+2\cdot\overrightarrow{NC}=\overrightarrow{0}\)
=>\(\overrightarrow{NE}+\overrightarrow{NC}=\overrightarrow{0}\)
=>N là trung điểm của CE
c: \(\left|\overrightarrow{PA}\right|=\left|\overrightarrow{PB}\right|\)
=>\(\left[{}\begin{matrix}\overrightarrow{PA}=-\overrightarrow{PB}\\\overrightarrow{PA}=\overrightarrow{PB}\left(loại\right)\end{matrix}\right.\)
=>\(\overrightarrow{PA}=-\overrightarrow{PB}\)
=>P là trung điểm của AB
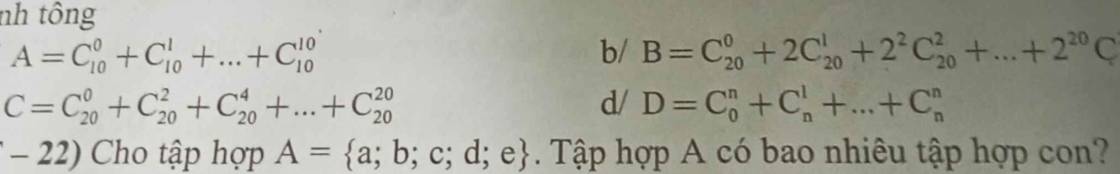
với ý d), ta có
TH1: \(a=0\)<=>\(m-1=0\)<=>\(m=1\)<=>PT trở thành PT bậc nhất 1 ẩn. Thay\(m=1\)vào PT, ta có
\(\left(1-1\right)x^2-\left(2.1-3\right)x+1+2=0\)<=>\(x+3=0\)<=>\(x=-3\)
TH2: \(a\ne0\)<=>\(m-1\ne0\)<=>\(m\ne1\), ta có
\(\Delta\ge0\)<=>\(\left(2m-3\right)^2-4\left(m+2\right)\left(m-1\right)\ge0\)
<=>\(4m^2-12m+9-4m^2+4m-8\ge0\)
<=>\(-8m+1\ge0\)
<=>\(m\le\frac{1}{8}\)
với \(m\le\frac{1}{8}\) và \(m=1\) làm cho PT trên có nghiệm