
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(\Leftrightarrow\left|x+1,5\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1,5=4\\x+1,5=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2,5\\x=-5,5\end{matrix}\right.\)
c)\(\Leftrightarrow-14+21x=5+10x\)
\(\Leftrightarrow11x=19\Leftrightarrow x=\dfrac{19}{11}\)

Bài 4:
a: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BM=CM
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔBAM có MA=MB
nên ΔBAM cân tại M
mà \(\widehat{B}=60^0\)
nên ΔBAM đều
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nen AM=BC/2
c: Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
mà MD là đường phân giác
nên MD là đường cao
=>MD⊥AC
mà AB⊥AC
nên MD//AB

Bài 4
\(a,x:y=3:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{5};y:z=4:5\Rightarrow\dfrac{y}{4}=\dfrac{z}{5}\\ \Rightarrow\dfrac{x}{12}=\dfrac{y}{20}=\dfrac{z}{25}=\dfrac{x+y+z}{12+20+25}=\dfrac{456}{57}=8\\ \Rightarrow\left\{{}\begin{matrix}x=96\\y=160\\z=200\end{matrix}\right.\)
\(b,a:b=2:3\Rightarrow\dfrac{a}{2}=\dfrac{b}{3};b:c=4:5\Rightarrow\dfrac{b}{4}=\dfrac{c}{5};c:d=6:7\Rightarrow\dfrac{c}{6}=\dfrac{d}{7}\\ \Rightarrow\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15};\dfrac{c}{6}=\dfrac{d}{7}\\ \Rightarrow\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\\ \Rightarrow\left\{{}\begin{matrix}a=32\\b=48\\c=60\\d=70\end{matrix}\right.\)


Ta có: A = |x - 2001| + |x - 1|
A = |x - 2001| + |1 - x| \(\ge\)|x - 2001 + 1 - x| = |-2000| = 2000
Dấu "=" xảy ra khi : x - 2001 + x - 1 = 0
<=> 2x - 2002 = 0
<=> 2x = 2002
<=> x = 1001
Vậy Min A = 2000 tại x = 1001

Câu 4:
Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|2y+3\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|2y+3\right|\ge0\forall x,y\)
Dấu '='xảy ra khi x=-2 và \(y=-\dfrac{3}{2}\)

Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC

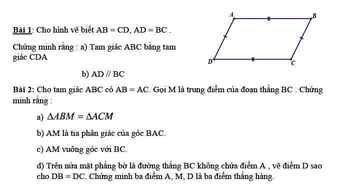
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)
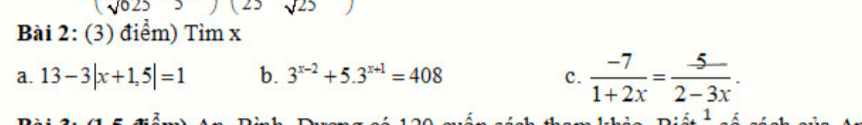
 giúp em câu 4,5,7 vs ạ em cảm ơn ;-;
giúp em câu 4,5,7 vs ạ em cảm ơn ;-;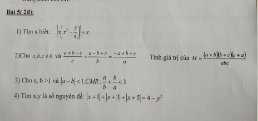

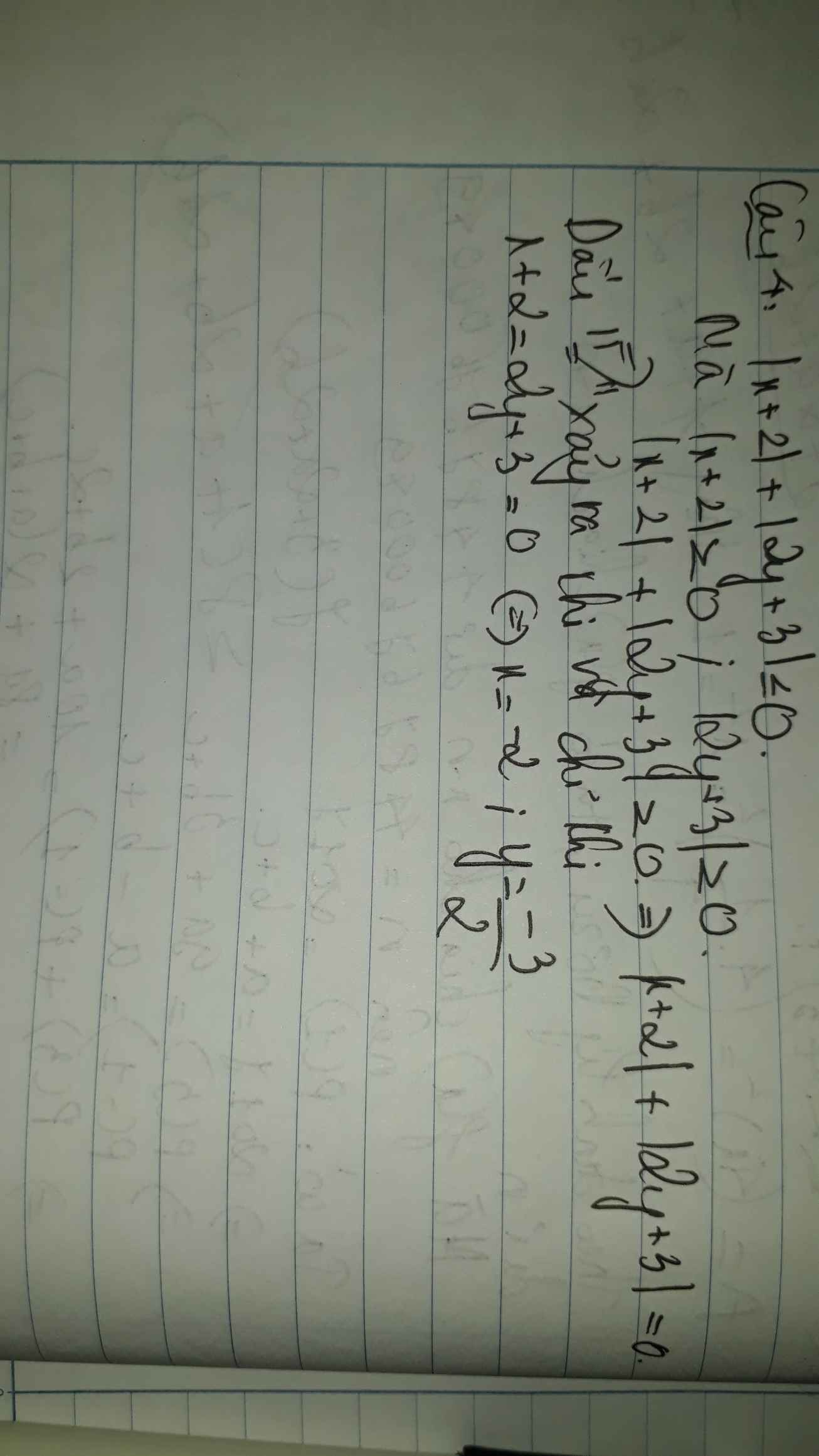

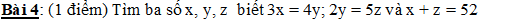
Lời giải:
Nếu $x+y+z=0$ thì:
$\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=0$
$\Rightarrow x=y=z=0$ (thỏa mãn)
Nếu $x+y+z\neq 0$ thì áp dụng tính chất dãy tỉ số bằng nhau:
$x+y+z=\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=\frac{x+y+z}{y+z+1+x+z+2+x+y-3}=\frac{x+y+z}{2(x+y+z)}=\frac{1}{2}$
Khi đó:
Từ điều kiện $\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}$
$\Rightarrow \frac{x}{x+y+z+1}=\frac{y}{x+y+z+2}=\frac{z}{x+y+z-3}$
$\Leftrightarrow \frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}=\frac{x+y+z}{\frac{3}{2}+\frac{5}{2}+\frac{-5}{2}}=\frac{\frac{1}{2}}{\frac{3}{2}}=\frac{1}{3}$
$\Rightarrow x=\frac{1}{2}; y=\frac{5}{6}; z=\frac{-5}{6}$
Chị ơi! Akai Haruma