K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
mọi người giải giúp em với ạ em đang cần gấp lắm ạ
0
NN
Mọi Người giải giúp em ạ em cảm ơn ạ
1
DA
1
TH
Giúp em với:((((
1
16 tháng 11 2021
\(2x+3y+5z=\frac{x^2+y^2+z^2}{2}+19\)
\(x^2+y^2+z^2+38=4x+6y+10z\)
\(\left(x^2-4x+4\right)+\left(y^2-6y+9\right)+\left(z^2-10z+25\right)=0\)
\(\left(x-2\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)
\(x-2=y-3=z-5=0\)
\(x=2,y=3,z=5\)
KT
1 tháng 10 2016
a) x(x-y)+(x-y)=(x+1)(x-y)
b) 2x+2y -x(x+y)= 2(x+y)-x(x+y)=(2-x)(x+y)
DM
0
Giúp em với ạ
4 tháng 3 2017
Ta có: \(\left(x-1\right)^2\ge0\) \(\Leftrightarrow x^2-2x+1\ge0\)\(\Leftrightarrow x^2+1\ge2x\).\(\left(1\right)\)
\(\left(y-2\right)^2\ge0\Leftrightarrow y^2-4y+4\ge0\Leftrightarrow x^2+4\ge4y\).\(\left(2\right)\)
\(\left(z^2-9\right)\ge0\Leftrightarrow z^2-6z+9\ge0\Leftrightarrow z^2+9\ge6z\).\(\left(3\right)\)
Từ \(\left(1\right),\left(2\right)\)và \(\left(3\right)\) nhân vế theo vế ta được:
\(\left(x^2+1\right).\left(y^2+4\right).\left(z^2+9\right)\ge48xyz\)
mà theo đề ta có:\(\left(x^2+1\right).\left(y^2+4\right).\left(z^2+9\right)=48xyz\)
nên \(\left\{{}\begin{matrix}x^2+1=2x\\y^2+4=4y\\z^2+9=6z\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\)
Thay \(x=1;y=2;z=3\)vào biểu thức A ta được:
\(A=\dfrac{x^3+y^3+z^3}{\left(x+y+z\right)^2}=\dfrac{1+8+27}{\left(1+2+3\right)^2}=1\)
Vậy giá trị của biểu thức \(A=\dfrac{x^3+y^3+z^3}{\left(x+y+z\right)^2}\)là 1.
giúp em bài với,em đang vội,mn giúp em ạ
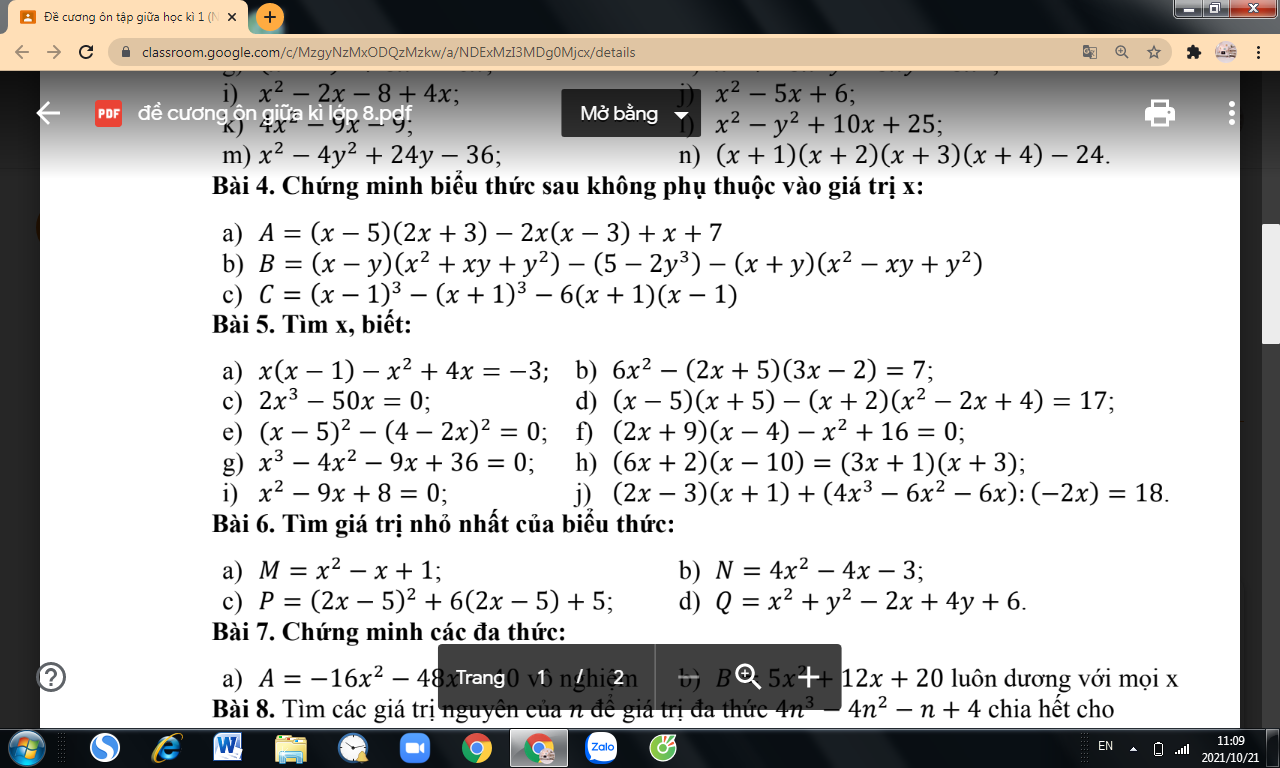
Bài 4:
b: \(B=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3-5-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3-y^3+2y^3-5-x^3-y^3\)
=-5
c: \(C=\left(x-1\right)^3-\left(x+1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6\left(x^2-1\right)\)
\(=-6x^2-2-6x^2+6\)
\(=-12x^2+4\)