K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
.png)
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)
H9
HT.Phong (9A5)
CTVHS
19 tháng 10 2023
a) Xét tứ giác ABCD ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{D}=360^o-102^o-102^o-102^o\)
\(\Rightarrow\widehat{D}=54^o\)
b) Xét tam giác vuông AOD ta có:
\(AD^2=OD^2+OA^2\)
\(\Rightarrow OA=\sqrt{AD^2-OD^2}\)
\(\Rightarrow OA=\sqrt{30^2-26,7^2}\approx13,7\left(cm\right)\)
Xét tam giác vuông AOB ta có:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow OB=\sqrt{AB^2-OA^2}\)
\(\Rightarrow OB=\sqrt{17,5^2-13,7^2}\approx10,9\left(cm\right)\)
Độ dài đường chéo BD là:
\(BD=OB+OD=26,7+10,9\approx37,6\left(cm\right)\)
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
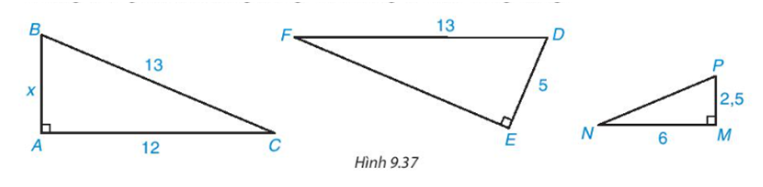
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)
DD
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
21 tháng 2 2023
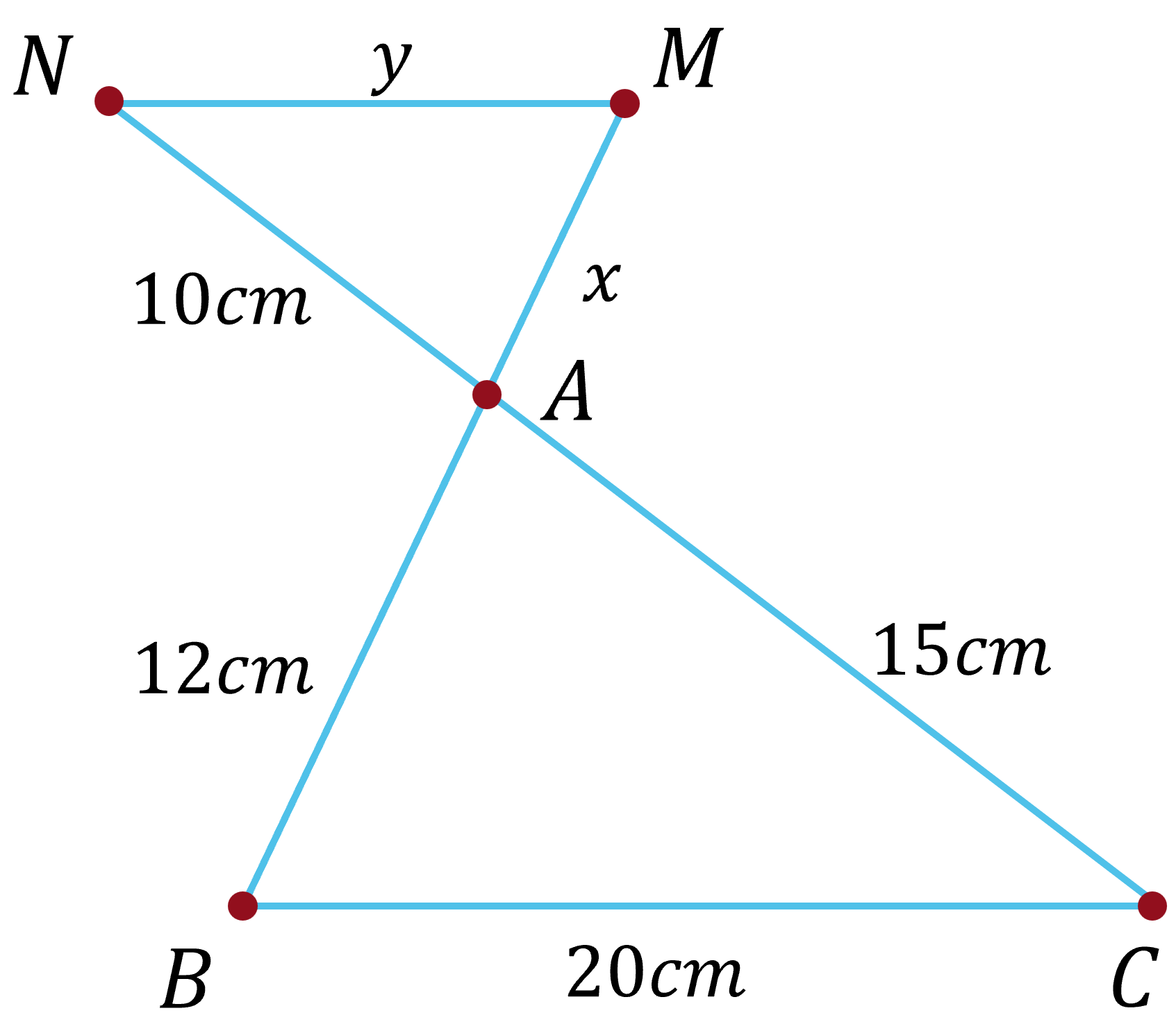
Vì MN // BC theo Talet ta có:
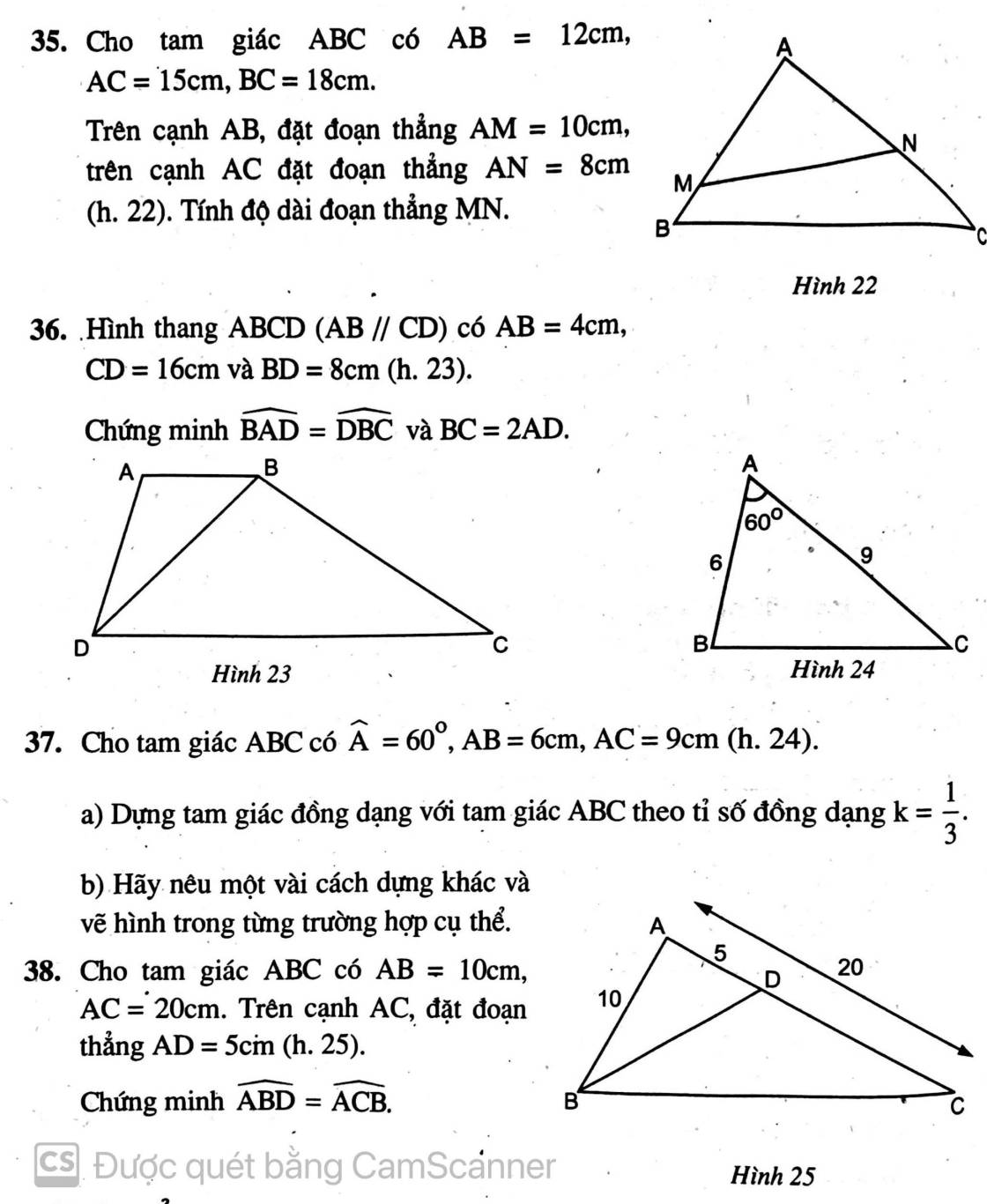
\(\dfrac{y}{20}\) = \(\dfrac{10}{15}\) = \(\dfrac{x}{12}\) => x = \(\dfrac{10}{15}\) . 12 = 8; y = \(\dfrac{10}{15}\) . 20 = \(\dfrac{40}{3}\)
KV
19 tháng 10 2023
a)
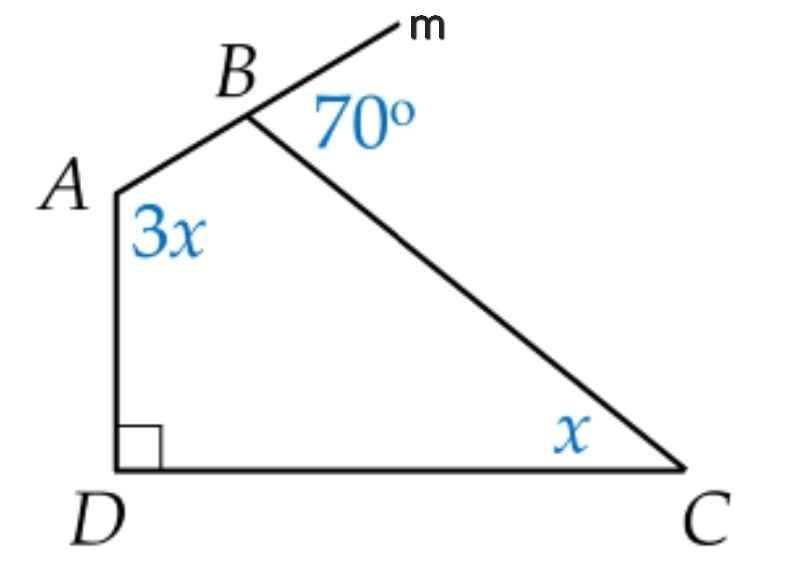Ta có:
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
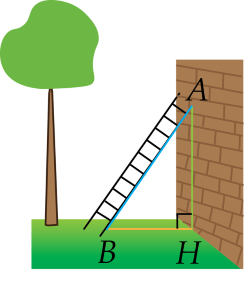
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
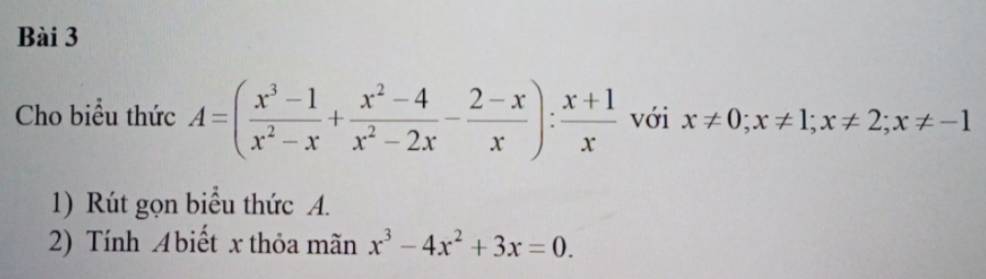
b: Sửa đề: AO vuông góc BI
Gọi M là trung điểm của IC
Xét ΔIHC có IO/IH=IM/IC
nên OM//HC và OM=1/2HC
=>OM vuông góc AH
Xet ΔAHM có
MO,HI là đường cao
MO cắt HI tại O
=>O là trực tâm
=>AO vuông góc HM
=>AO vuông góc BI