Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(P) tiếp xúc với (S) nên P và S phải có điểm chung duy nhất là M
thay tọa độ M vào các phương trình thử thì
Câu A đúng
M∈ (S) : (x0 - 2)2 + (y0-1)2 +(z0-1)2 =9.
A=x0+2y0+2z0=(x0-2)+2(y0-1)+2(z0-1)+6
Dùng BĐT bunhiacopski
[(x0-2)+2(y0-1)+2(z0-1)]2 ≤ (1+4+4).[(x0 - 2)2 + (y0-1)2 +(z0-1)2 ]
≤ 81
-9 ≤ (x0-2)+2(y0-1)+2(z0-1) ≤ 9.
-3 ≤ A ≤ 12. vậy GTNN của A = -3.
Dấu bằng xảy ra khi :
x0+2y0+2z0 = -3
và \(\dfrac{x0-2}{1}=\dfrac{y0-1}{1}=\dfrac{z0-1}{1}\)
Giải hệ được x0=1, y0=z0=-1. Suy ra: x0+y0+z0 = -1
Gọi \(N\left(4;-1;-3\right)\Rightarrow2\overrightarrow{NA}-\overrightarrow{NB}=0\)
\(2MA^2-MB^2=4\)
\(\Leftrightarrow2\left(\overrightarrow{MN}+\overrightarrow{NA}\right)^2-\left(\overrightarrow{MN}+\overrightarrow{NB}\right)^2=4\)
\(\Leftrightarrow MN^2+2NA^2-NB^2+2\overrightarrow{MN}\left(2\overrightarrow{NA}-\overrightarrow{NB}\right)=4\)
\(\Leftrightarrow MN^2=4+NB^2-2NA^2=28\)
\(\Rightarrow MN=2\sqrt{7}\Rightarrow\) M thuộc mặt cầu (C) tâm N bán kính \(R=2\sqrt{7}\) có pt:
\(\left(x-4\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=28\)
Mà \(M\in\left(P\right)\Rightarrow\) quỹ tích M là đường tròn giao tuyến của mặt phẳng (P) và mặt cầu (C)
Theo định lý Pitago: \(r=\sqrt{R^2-d^2}\) với \(d\) là khoảng cách từ N tới mặt phẳng (P)
Bạn tự tính và thay số nốt đoạn còn lại.
Phương trình dạng tham số của d: \(\left\{{}\begin{matrix}x=-1+2t\\y=1-t\\z=2t\end{matrix}\right.\)
Do \(M\in d\) nên tọa độ thỏa mãn \(\left\{{}\begin{matrix}a=-1+2t\\b=1-t\\z=2t\end{matrix}\right.\)
\(A=\left(a+1\right)^2+b^2+c^2=\left(-1+2t+1\right)^2+\left(1-t\right)^2+4t^2\)
\(=9t^2-2t+1=9\left(t-\frac{1}{9}\right)^2+\frac{8}{9}\ge\frac{1}{9}\)
Dấu "=" xảy ra khi \(t=\frac{1}{9}\Rightarrow\left\{{}\begin{matrix}a=-\frac{7}{9}\\b=\frac{8}{9}\\c=\frac{2}{9}\end{matrix}\right.\) \(\Rightarrow T=0\)
Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó 
Ta có:
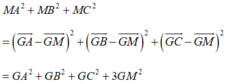
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto 
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.
a. 32x - 5.(3.2)x + 22x.4 =0
(=) \(\left(\dfrac{3}{2}\right)^{^{2x}}-5.\left(\dfrac{3}{2}\right)^x+2^{2x}.4\) =0
đặt \(\left(\dfrac{3}{2}\right)^x=t\) đk: t > 0
=> pttt: t2 - 5t +4 =0
(=)\(\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
(=) \(\left[{}\begin{matrix}\left(\dfrac{3}{2}\right)^x=1\\\left(\dfrac{3}{2}\right)^x=4\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{3}{2}}4\end{matrix}\right.\)
b. 3.52x + 2.72x - 5.(5.7)x =0
(=) \(3+2.\left(\dfrac{7}{5}\right)^{2x}-5.\left(\dfrac{7}{5}\right)^x=0\)
đặt \(t=\left(\dfrac{7}{5}\right)^x\) đk: t > 0
pttt: 3+2t2-5t=0
(=) \(\left[{}\begin{matrix}t=1\\t=\dfrac{3}{2}\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{7}{5}}\dfrac{3}{2}\end{matrix}\right.\)
Chọn A
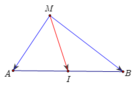
Gọi I, O lần lượt là trung điểm của AB và IC, khi đó với điểm M bất kỳ ta luôn có
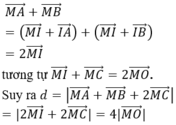
nên d nhỏ nhất khi và chỉ khi 
nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
Đường thẳng qua O (0;0;0) vuông góc với (P) có phương trình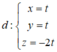 
Giao điểm của d và (P) chính là hình chiếu vuông góc M của O (0;0;0) lên mặt phẳng (P).
Thay toạ độ A; B vào (P) thấy ra kết quả cùng dấu, vậy A và B nằm cùng phía so với (P)
Gọi C là điểm đối xứng A qua (P) thì MA+MB nhỏ nhất khi và chỉ khi M trùng giao điểm của BC và (P)
Phương trình đường thẳng d qua A và vuông góc (P): \(\left\{{}\begin{matrix}x=2+t\\y=2t\\z=3+2t\end{matrix}\right.\)
Giao điểm D của d và (P) là nghiệm:
\(2+t+2\left(2t\right)+2\left(3+2t\right)+1=0\Rightarrow t=-1\Rightarrow D\left(1;-2;1\right)\)
\(\overrightarrow{AD}=\left(-1;-2;-2\right)\) mà \(\overrightarrow{AD}=\overrightarrow{DC}\Rightarrow C\left(0;-4;-1\right)\)
\(\overrightarrow{CB}=\left(3;3;6\right)\Rightarrow\overrightarrow{u_{BC}}=\left(1;1;2\right)\Rightarrow\) pt BC: \(\left\{{}\begin{matrix}x=3+t\\y=-1+t\\z=5+2t\end{matrix}\right.\)
Toạ độ M là nghiệm:
\(3+t+2\left(1-t\right)+2\left(5+2t\right)+1=0\Rightarrow t=-\frac{12}{7}\Rightarrow M\left(\frac{9}{7};-\frac{19}{7};\frac{11}{7}\right)\)
\(\Rightarrow T=\frac{563}{49}\)
e cám ơn