Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N P Q
Có: AM=BM(gt)
AN=CN(gt)
=>PQ là đường trung bình của ht BMNC
=>PQ//MN
Bên dưới giải thiếu
Xét ΔABC có:
AM=BM(gt)
AN=CN(gt)
=>MN là đường trung bình
=>MN//BC
=>BMNC là hình thnag
(Xong nối đoạn dưới vào)

Ta có: (AB+DC):2 = MN ( đường trung bình của hình thang)
=> AB+DC = MN.2 = 3.2 =6
AB = 6 - DC = 6 - 4 =2
=> AB=2

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA/10=OC/18=(OA+OC)/(10+18)=21/28=3/4
=>OA=7,5cm; OC=13,5cm
b: OA/OC=OB/OD
=>OA*OD=OB*OC
c: AM/CN=AB/CD=OA/OC
Xét ΔOAM và ΔOCN có
OA/OC=AM/CN
góc OAM=góc OCN
=>ΔOAM đồng dạng với ΔOCN
=>góc AOM=góc CON
=>góc AOM+góc AON=180 độ
=>M,O,N thẳng hàng

a: Kẻ BK vuông góc với AD
=>BKDC là hình chữ nhật
=>BK=DC=40m; CB=DK=6m
=>AK=9m
\(AB=\sqrt{40^2+9^2}=41\left(m\right)\)
b: \(AC=\sqrt{15^2+40^2}=5\sqrt{73}\left(cm\right)\)
\(cosABC=\dfrac{BC^2+BA^2-AC^2}{2\cdot BC\cdot BA}=\dfrac{-9}{41}\)
=>\(sinABC=\dfrac{40}{41}\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot41\cdot\dfrac{40}{41}=3\cdot40=120\left(cm^2\right)\)


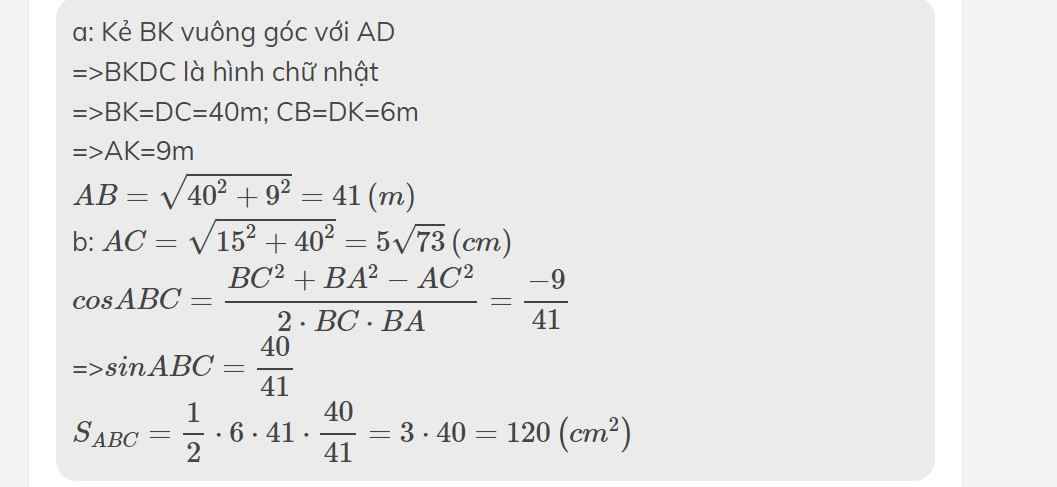
AB=150m