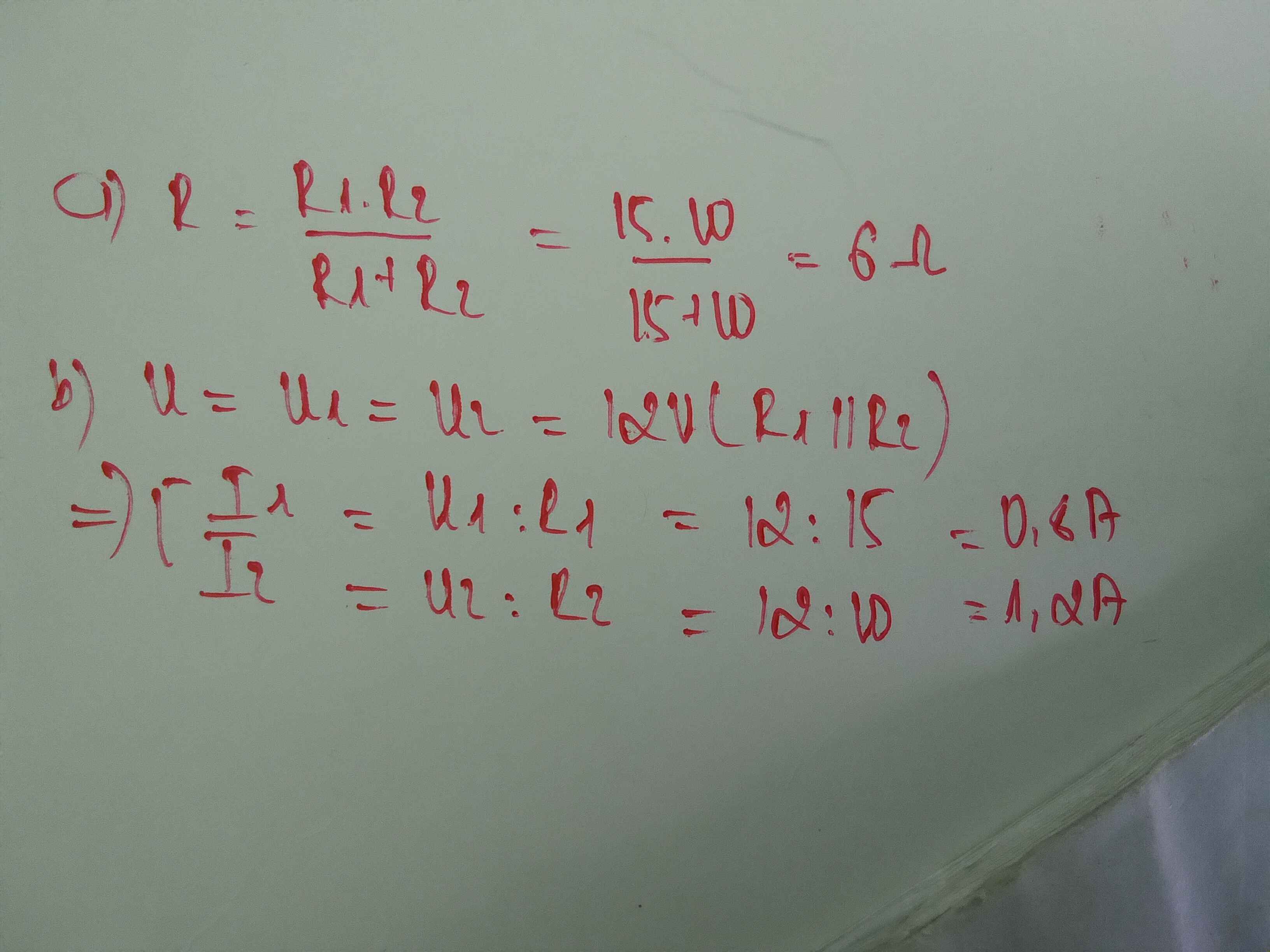Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở tương đương của đoạn mạch:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12.24}{12+24}=8\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=12V\)
Cường độ dòng điện chạy qua mỗi điện trở và qua mạch chính:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{12}{8}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{12}{12}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{24}=0,5\left(A\right)\end{matrix}\right.\)

Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{30.60}{30+60}=20\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=30V\)
Cường độ dòng điện chạy qua mạch chính và mỗi mạch rẽ:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{30}{20}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{30}{30}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{30}{60}=0,5\left(A\right)\end{matrix}\right.\)
Điện trở tương đương lúc này là:
\(R_{tđ}=R_{12}+R_3=20+40=60\left(\Omega\right)\)
Do mắc nối tiếp nên \(I=I_{12}=I_3=1,5\left(A\right)\)
Nhiệt năng đoạn mạch tiêu thụ trong 30ph:
\(A=P.t=I^2.R.t=1,5^2.60.30.60=243000\left(J\right)\)
Nhiệt lượng tỏa ra của R3 trong 30ph:
\(Q_{tỏa_3}=A_3=I_3^2.R_3.t=1,5^2.40.30.60=162000\left(J\right)\)

Vì R 1 mắc song song R 2 nên: U 1 = U 2 ⇔ I 1 . R 1 = I 1 . R 2
Mà I 1 = 1,5 I 2 → 1,5 I 2 . R 1 = I 2 . R 2 → 1,5 R 1 = R 2
Từ (1) ta có R 1 + R 2 = 10Ω (2)
Thay R 2 = 1,5 R 1 vào (2) ta được: R 1 + 1,5 R 1 = 10 ⇒ 2,5 R 1 = 10 ⇒ R 1 = 4Ω
⇒ R 2 = 1,5.4 = 6Ω

a, Khi 3 điện trở mắc song song thì UAB=U1=U2=U3
=> I1R1=I2R2=I3R3 => 3R1 = R2 = 1,5R3
=> R2 = 3R1 ; R3= 2R1
Khi 3 điệm trở mắc nối tiếp Rm=R1+R2+R3=6R1
=> Cường độ dòng điện chạy qua mỗi điện trở là:
I1=I2=I3= UAB/(6R1) = 3/6=1/2 (A)

a. Bạn tự vẽ sơ đồ mạch điện nhé!
\(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.5}{10+5}=\dfrac{10}{3}\left(\Omega\right)\)
b. \(U=U1=U2=12V\)(R1//R2)
\(\left[{}\begin{matrix}I1=U1:R1=12:10=1,2A\\I2=U2:R2=12:5=2,4A\end{matrix}\right.\)
\(\left[{}\begin{matrix}P1=U1.I1=12.1,2=14,4\left(W\right)\\P2=U2.I2=12.2,4=28,8\left(W\right)\end{matrix}\right.\)
c. \(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{10}+\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{1}{2}\Rightarrow R=2\left(\Omega\right)\)
\(U=U1=U2=U3=12V\)(R1//R2//R3)
\(\left[{}\begin{matrix}I1=U1:R1=12:10=1,2A\\I2=U2:R2=12:5=2,4A\\I3=U3:R3=12:5=2,4A\end{matrix}\right.\)

a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.15}{10+15}=6\left(\Omega\right)\)
b. \(U=U1=U2=12\left(V\right)\)(R1//R2)
\(\left[{}\begin{matrix}I=U:R=12:6=2\left(A\right)\\I1=U1:R1=12:10=1,2\left(A\right)\\I2=U2:R2=12:15=0,8\left(A\right)\end{matrix}\right.\)