Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAI vuôg tại A và ΔOBI vuông tại B có
OI chung
góc AOI=góc BOI
Do đó: ΔOAI=ΔOBI
Suy ra: OA=OB
b: Xét ΔIAM vuông tại A và ΔIBN vuông tại B có
IA=IB
góc AIM=góc BIN
Do đó: ΔIAM=ΔIBN
Suy ra: IM=IN

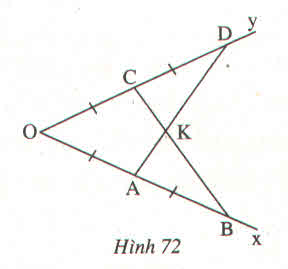
Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)

Câu 1:\(\dfrac{15-x}{5-x}\) điều kiện \(x\ne5\)
Để \(\dfrac{15-x}{5-x}\) đạt giá trị lớn nhất thì \(5-x\) là số nguyên dương nhỏ nhất có thể.
\(\Rightarrow5-x=1\Rightarrow x=4\)
Thay vào ta có: \(\dfrac{15-4}{5-4}=\dfrac{11}{1}=11\)
Vậy GTLN của biểu thức là 11 đạt được khi và chỉ khi \(x=4\)
Câu 2: \(\dfrac{5x-19}{x-4}\) (điều kiện \(x\ne4\))
Để \(\dfrac{5x-19}{x-4}\) đạt giá trị nhỏ nhất thì \(x-4\) là số nguyên âm lớn nhất có thể.
\(\Rightarrow x-4=-1\Rightarrow x=3\)
Thay vào ta có: \(\dfrac{5x-19}{x-4}=\dfrac{5.3-19}{3-4}=\dfrac{15-19}{-1}=\dfrac{-4}{-1}=4\)
Vậy GTNN của biểu thức là 4 đạt được khi và chỉ khi x=3
Chúc bạn học tốt!!!
\(\dfrac{15-x}{5-x}\)
\(MAX_{\dfrac{15-x}{5-x}}\Rightarrow\dfrac{15-x}{5-x}\in Z^+;5-x_{MIN}\)
\(\Rightarrow5-x=1\)
\(\Rightarrow x=4\)
\(\Rightarrow MAX_{\dfrac{15-x}{5-x}}=\dfrac{15-4}{5-4}=11\)

a: Bổ sung đề OA=OB
Xét ΔAOC và ΔBOC có
OC chung
OA=OB
AC=BC
Do đó: ΔAOC=ΔBOC
Xét ΔOAD và ΔOBD có
OA=OB
OD chung
AD=BD
Do đó ΔOAD=ΔOBD
b: Ta có: OA=OB
nên O nằm trên đường trung trực của AB(1)
Ta có: CA=CB
nên C nằm trên đường trung trực của AB(2)
Ta có: DA=DB
nên D nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,C,D thẳng hàng

Là ở đâu?
Ở linh trên