D
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 3 2016
<=><=>(X+1)(Y+1)=6 và (x+1)^3+(y+1)^3=35đặt X+1;Y+1 biến đổi vế 2 giải ra đc(1;2);(2;1)
b,<=>\(\left[\sqrt{2}+1\right]^x+\left[\sqrt{2}-1\right]^x=6\)
<=>\(2\sqrt{2}^x+2=6\)
<=>x=2
A
0
1 tháng 1 2023
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{5}\left(1-\sqrt{3}\right)x-y\cdot\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)=1-\sqrt{3}\\\left(1-\sqrt{3}\right)\cdot x\cdot\sqrt{5}+5y=\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{5}-\sqrt{15}\right)x+2y=1-\sqrt{3}\\\left(\sqrt{5}-\sqrt{15}\right)x+5y=\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3y=1-\sqrt{3}-\sqrt{5}\\\left(\sqrt{5}-\sqrt{15}\right)x+5y=\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x\left(\sqrt{5}-\sqrt{15}\right)=\sqrt{5}-\dfrac{5}{3}\left(-1+\sqrt{3}+\sqrt{5}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x\left(\sqrt{5}-\sqrt{15}\right)=\dfrac{5}{3}-\dfrac{5}{3}\sqrt{3}-\dfrac{2}{3}\sqrt{5}=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3\left(\sqrt{5}-\sqrt{15}\right)}=\dfrac{\sqrt{5}-\sqrt{15}-2}{3\left(1-\sqrt{3}\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3\left(\sqrt{5}-\sqrt{15}\right)}=\dfrac{\sqrt{5}-\sqrt{15}-2}{3\left(1-\sqrt{3}\right)}=\dfrac{\sqrt{15}-\sqrt{5}+2}{3\left(\sqrt{3}-1\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{5}+\sqrt{3}-1}{3}\\y=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)+2\left(\sqrt{3}+1\right)}{6}=\dfrac{\sqrt{5}+\sqrt{3}+1}{3}\end{matrix}\right.\)
20 tháng 12 2019
a/ (1−\(\sqrt{2}\))x2 −2(1+\(\sqrt{2}\))x+1+3\(\sqrt{2}\)=0
⇔ (1−\(\sqrt{2}\)) (x2 - 2x +3) = 0 (Đặt nhân tử chung)
⇔ 1- \(\sqrt{2}\) = 0 và x2 -2x +3 = 0
b) nhân 6 với \(\sqrt{2}\)+1 là ra phương trình bậc 2
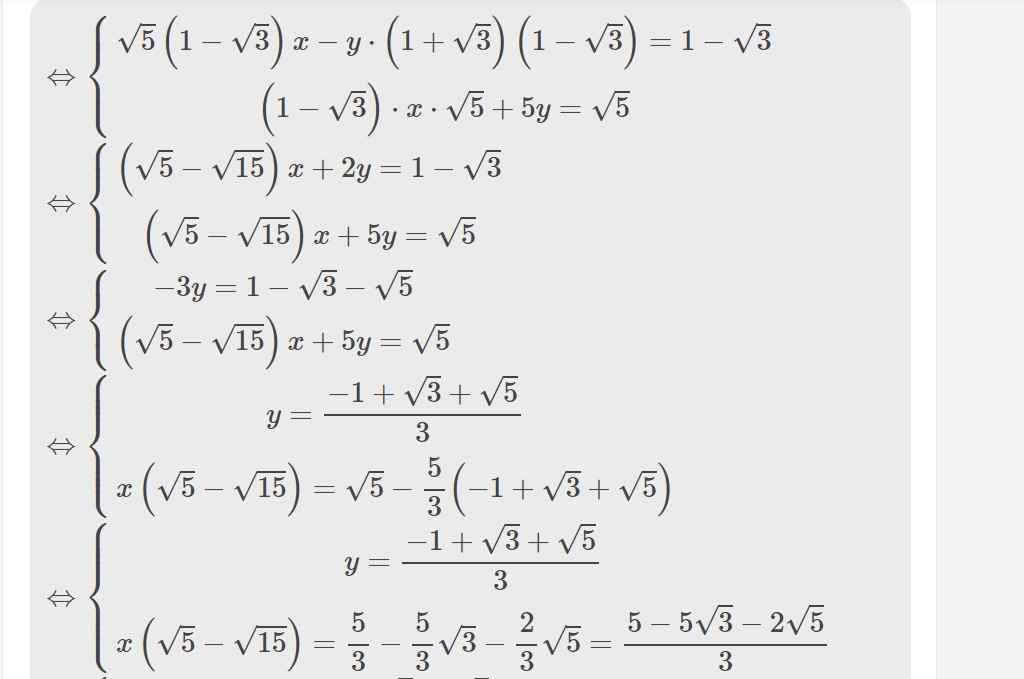
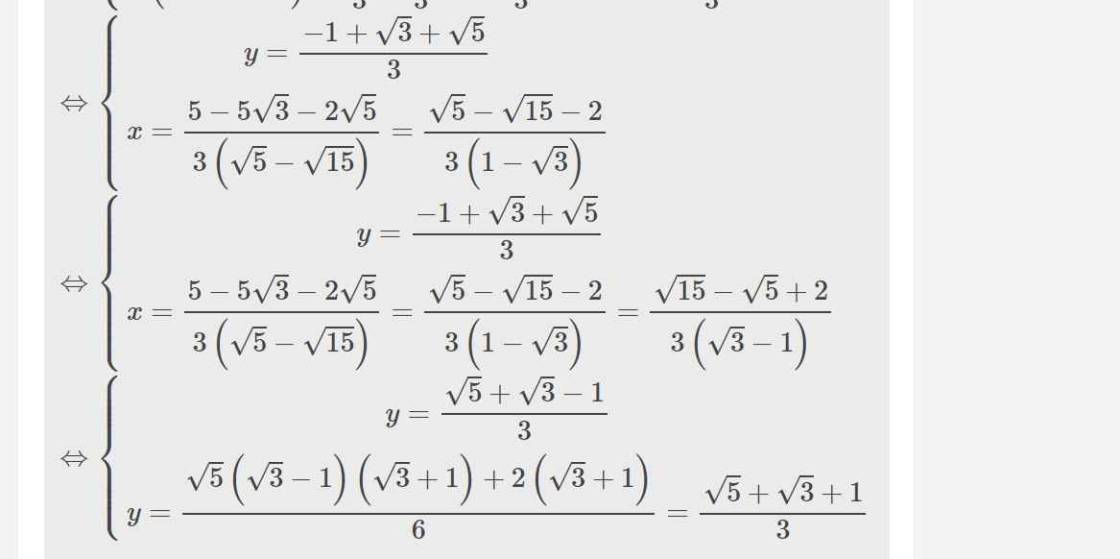
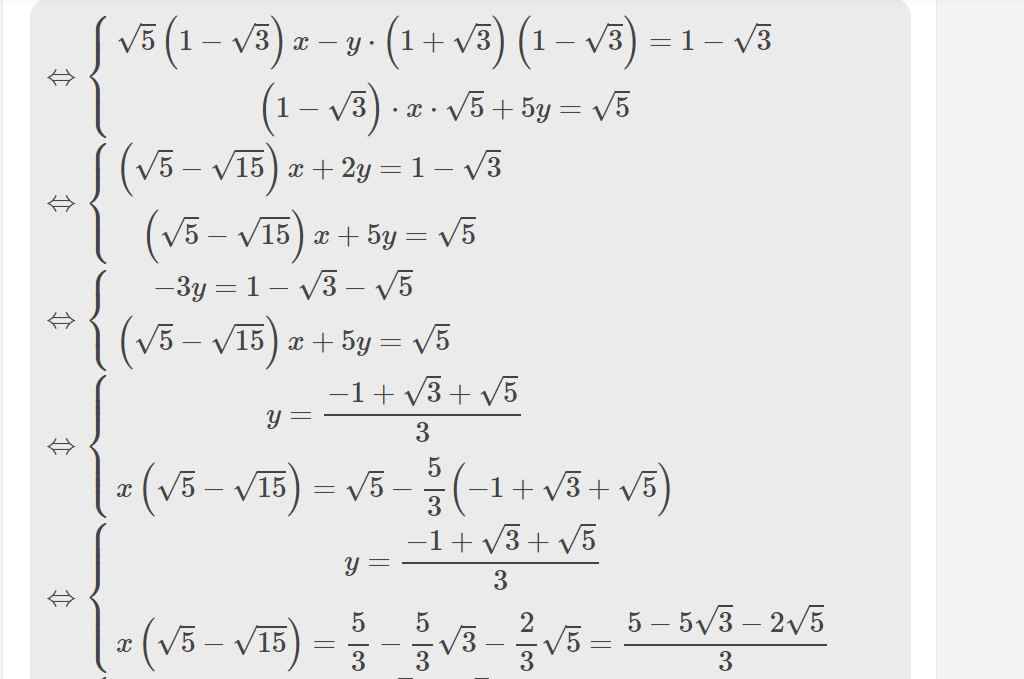
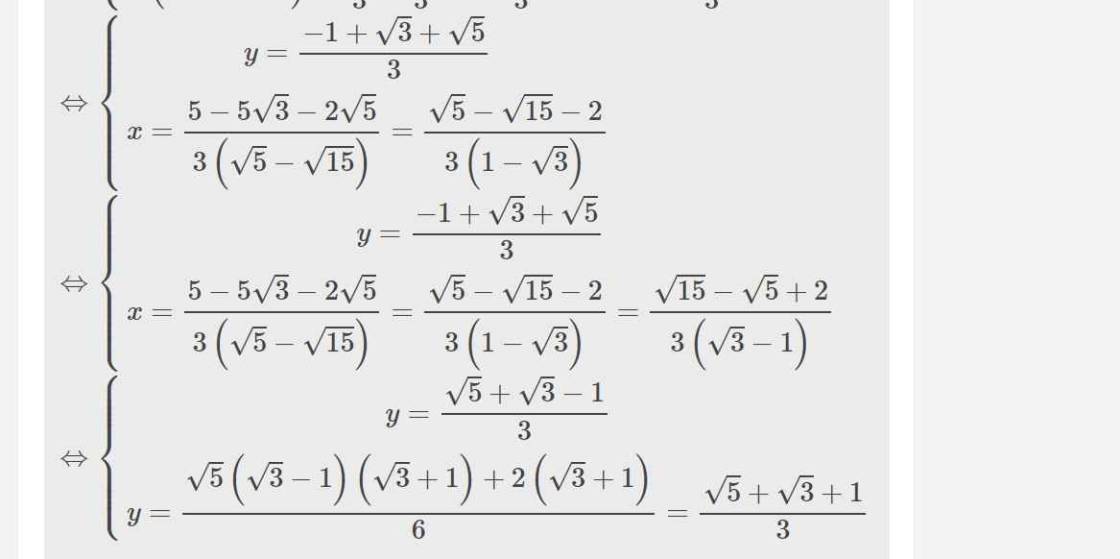
\(\sqrt{\left(x-1\right)\left(x-5\right)}-3\sqrt{1-x}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)\ge0\\1-x\ge0\\\sqrt{\text{}\left(x-1\right)\left(x-5\right)}=3\sqrt{1-x}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x-5\ge0\\x-1\le0\end{matrix}\right.\\x\le1\\\sqrt{\text{}\left(x-1\right)\left(x-5\right)}=3\sqrt{1-x}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge5\\x\le1\end{matrix}\right.\\x\le1\\\left(x-1\right)\left(x-5\right)=9\left(1-x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left(x-1\right)\left(x-5\right)+9\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left(x-1\right)\left(x-5+9\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left(x-1\right)\left(x+4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)
- Vậy \(S=\left\{1;-4\right\}\)
\(\sqrt{1-x}(\sqrt{5-x}-3)=0\)
x = 1 hay \(\sqrt{5-x}=3 \)
x = 1 hay x= - 4