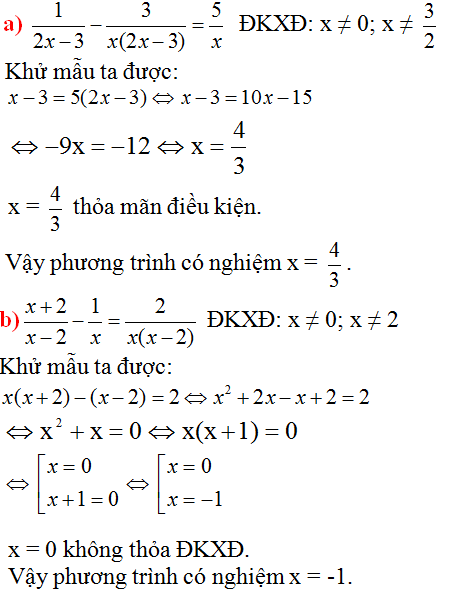Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


giải luôn ko chép đề nhé
a,
<=>(3x-5)(x-1)=(3x+1)(x-2)-3(x-1)
<=>3x^2-8x+5=3x^2-5x-2-3x+3
<=>3x^2-8x-3x^2+5x+3x=-5+3
<=>0x=-2
vậy s=\(\varnothing\)

a: \(\Leftrightarrow1-x+3x+3=2x+3\)
=>2x+4=2x+3(vô lý)
b: \(\Leftrightarrow\left(x+2\right)^2-2x+3=x^2+10\)
\(\Leftrightarrow x^2+4x+4-2x+3=x^2+10\)
=>4x+7=10
hay x=3/4
d: \(\Leftrightarrow\left(-2x+5\right)\left(3x-1\right)+3\left(x-1\right)\left(x+1\right)=\left(x+2\right)\left(1-3x\right)\)
\(\Leftrightarrow-6x^2+2x+15x-5+3\left(x^2-1\right)=\left(x+2\right)\left(1-3x\right)\)
\(\Leftrightarrow-6x^2+17x-5+3x^2-3=x-3x^2+2-6x\)
\(\Leftrightarrow-3x^2+17x-8=-3x^2-5x+2\)
=>22x=10
hay x=5/11

a. (x + 2)(x2 – 3x + 5) = (x + 2)x2
⇔ (x + 2)(x2 – 3x + 5) – (x + 2)x2 = 0
⇔ (x + 2)[(x2 – 3x + 5) – x2] = 0
⇔ (x + 2)(\(x^2\) – 3x + 5 – \(x^2\)) = 0
⇔ (x + 2)(5 – 3x) = 0
⇔ x + 2 = 0 hoặc 5 – 3x = 0
x + 2 = 0 ⇔ x = -2
5 – 3x = 0 ⇔ x = \(\dfrac{5}{3}\)
Vậy phương trình có nghiệm x = -2 hoặc x =\(\dfrac{5}{3}\)
c.\(2x^2\) – x = 3 – 6x
⇔ \(2x^2\) – x + 6x – 3 = 0
⇔ (\(2x^2\) + 6x) – (x + 3) = 0
⇔ 2x(x + 3) – (x + 3) = 0
⇔ (2x – 1)(x + 3) = 0
⇔ 2x – 1 = 0 hoặc x + 3 = 0
2x – 1 = 0 ⇔ x = 1/2
x + 3 = 0 ⇔ x = -3
Vậy phương trình có nghiệm x = \(\dfrac{1}{2}\) hoặc x = -3

a) 1x−1−3x2x3−1=2xx2+x+11x−1−3x2x3−1=2xx2+x+1
Ta có: x3−1=(x−1)(x2+x+1)x3−1=(x−1)(x2+x+1)
=(x−1)[(x+12)2+34]=(x−1)[(x+12)2+34] cho nên x3 – 1 ≠ 0 khi x – 1 ≠ 0⇔ x ≠ 1
Vậy ĐKXĐ: x ≠ 1
Khử mẫu ta được:
x2+x+1−3x2=2x(x−1)⇔−2x2+x+1=2x2−2xx2+x+1−3x2=2x(x−1)⇔−2x2+x+1=2x2−2x
⇔4x2−3x−1=0⇔4x2−3x−1=0
⇔4x(x−1

a ) \(\dfrac{1}{x+1}-\dfrac{5}{x-2}=\dfrac{15}{\left(x+1\right)\left(2-x\right)}\)(1)
ĐKXĐ : \(x\ne1;x\ne2\)
(1)\(\Leftrightarrow\dfrac{1}{x+1}+\dfrac{5}{2-x}=\dfrac{15}{\left(x+1\right)\left(2-x\right)}\)
\(\Leftrightarrow2-x+5x+5=15\)
\(\Leftrightarrow4x+7=15\\\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(KTMĐKXĐ\right)\)
Vậy pt vô nghiệm .
b ) \(1+\dfrac{x}{3-x}=\dfrac{5x}{\left(x+2\right)\left(3-x\right)}+\dfrac{2}{x+2}\) ( 2 )
ĐKXĐ : \(x\ne3;x\ne-2\)
(2) \(\Leftrightarrow3x-x^2+6-2x+x^2+2x=3x+6-x^2-2x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(TMĐKXĐ\right)\\x=-2\left(KTMĐKXĐ\right)\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là S={0}.
c ) \(\dfrac{6}{x-1}-\dfrac{4}{x-3}=\dfrac{8}{\left(x-1\right)\left(3-x\right)}\) (3)
ĐKXĐ : \(x\ne1;x\ne3\)
\(\left(3\right)\Leftrightarrow\dfrac{6}{x-1}+\dfrac{4}{3-x}=\dfrac{8}{\left(x-1\right)\left(3-x\right)}\)
\(\Leftrightarrow6\left(3-x\right)+4\left(x-1\right)=8\)
\(\Leftrightarrow18-6x+4x-4=8\)
\(\Leftrightarrow-2x=6\)
\(\Leftrightarrow x=-3\)
Vậy tập nghiệm của phương trình là S={-3}
d ) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\) (4)
ĐKXĐ : \(x\ne0;x\ne2\)
\(\left(4\right)\Leftrightarrow x^2+2x-x+2=2\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(KTMĐKXĐ\right)\\x=-1\left(TMĐKXĐ\right)\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là S={-1}
a) \(\dfrac{1}{x+1}-\dfrac{5}{x-2}=\dfrac{15}{\left(x+1\right)\left(2-x\right)}\) ( đk: x ≠ -1; x ≠ 2 )
\(\Leftrightarrow\) \(\dfrac{1}{x+1}+\dfrac{5}{2-x}=\dfrac{15}{\left(x+1\right)\left(2-x\right)}\)
\(\Leftrightarrow\) \(2-x+5\left(x+1\right)=15\)
\(\Leftrightarrow\) \(2-x+5x+5=15\)
\(\Leftrightarrow\)\(4x=8\)
\(\Rightarrow\) \(x=2\) ( KTM )
S = ∅
b) \(1+\dfrac{x}{3-x}=\dfrac{5x}{\left(x+2\right)\left(3-x\right)}+\dfrac{2}{x+2}\) ( đk: x ≠ - 2 ; x ≠ 3 )
\(\Leftrightarrow\) \(\left(x+2\right)\left(3-x\right)+x\left(x+2\right)=5x+2\left(3-x\right)\)
\(\Leftrightarrow\) \(3x-x^2+6-2x+x^2+2x=5x+6-2x\)
\(\Leftrightarrow\) \(3x+6=3x+6\)
\(\Rightarrow\)\(0x=0\) ( TM )
\(\Rightarrow\) Phương trình vô số nghiệm
S = R
c) \(\dfrac{6}{x-1}-\dfrac{4}{x-3}=\dfrac{8}{\left(x-1\right)\left(3-x\right)}\) ( đk: x ≠ 1 ; x ≠ 3 )
\(\Leftrightarrow\) \(\dfrac{6}{x-1}+\dfrac{4}{3-x}=\dfrac{8}{\left(x-1\right)\left(3-x\right)}\)
\(\Leftrightarrow\)\(6\left(3-x\right)+4\left(x-1\right)=8\)
\(\Leftrightarrow\) \(18-6x+4x-4=8\)
\(\Leftrightarrow\) \(-2x=-6\)
\(\Rightarrow x=3\) ( KTM )
S = ∅
d) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\) (đk: x ≠ 2; x ≠ 0 )
\(\Leftrightarrow\) \(x\left(x+2\right)-x+2=2\)
\(\Leftrightarrow\) \(x^2+2x-x+2=2\)
\(\Leftrightarrow\) \(x^2+x=0\)
\(\Leftrightarrow\) \(x\left(x+1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\)
S = \(\left\{2\right\}\)