Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đk: \(x\ge2\)
pt <=> \(\frac{4\left(x+2\right)-\left(4x+1\right)}{2\sqrt{x+2}+\sqrt{4x+1}}\left(2x+3+\sqrt{4x^2+9x+2}\right)=7\)
<=> \(\frac{7}{2\sqrt{x+2}+\sqrt{4x+1}}\left(2x+3+\sqrt{4x^2+9x+2}\right)=7\)
<=> \(2x+3+\sqrt{4x^2+9x+2}=2\sqrt{x+2}+\sqrt{4x+1}\)(1)
Đặt : \(t=2\sqrt{x+2}+\sqrt{4x+1}\ge0\)
Ta có: \(t^2=8x+9+4\sqrt{4x^2+9x+2}\)<=> \(2x+3+\sqrt{4x^2+9x+2}=\frac{t^2+3}{4}\)
Phương trình (1) trở thành: \(\frac{t^2+3}{4}=t\Leftrightarrow t^2-4t+3=0\Leftrightarrow\orbr{\begin{cases}t=3\\t=1\end{cases}\left(tm\right)}\)
+) Với t = 1. Ta có:
\(2\sqrt{x+2}+\sqrt{4x+1}=1\)
<=> \(8x+9+4\sqrt{4x^2+9x+2}=1\)
<=> \(\sqrt{4x^2+9x+2}=-2-2x\)
<=> \(\hept{\begin{cases}-2-2x\ge0\\4x^2+9x+2=4x^2+8x+4\end{cases}\Leftrightarrow}\hept{\begin{cases}x\le-1\\x=2\end{cases}}\)loại
+) Với t = 3. Ta có:
\(2\sqrt{x+2}+\sqrt{4x+1}=3\)
<=> \(8x+9+4\sqrt{4x^2+9x+2}=9\)
<=> \(\sqrt{4x^2+9x+2}=-2x\)
<=> \(\hept{\begin{cases}-2x\ge0\\4x^2+9x+2=4x^2\end{cases}\Leftrightarrow}\hept{\begin{cases}x\le0\\9x+2=0\end{cases}}\Leftrightarrow x=-\frac{2}{9}\left(tmdk\right)\)
Vây:...
ĐK \(x\ge\frac{-1}{4}\)
Với điều kiện đó ta có \(2\sqrt{x+2}+\sqrt{4x+1}>0\)
Biến đổi phương trình đã cho trở thành
\(7\left(2x+3+\sqrt{4x^2+9x+2}\right)7\left(2\sqrt{x+2}+\sqrt{4x+1}\right)\)
\(\Leftrightarrow2x+3+\sqrt{4x^2+9x+2}=2\sqrt{x+2}+\sqrt{4x+1}\left(1\right)\)
Đặt \(t=2\sqrt{x+2}+\sqrt{4x+1}\left(t\ge\sqrt{7}\right)\)
\(t^2=8x+9+4\sqrt{4x^2+9x+2}\Rightarrow2x+\sqrt{4x^2+9x+2}=\frac{t^2-9}{4}\)
Thay vào (1) ta được \(t^2-4t+3=0\Leftrightarrow\orbr{\begin{cases}t=1\left(ktm\right)\\t=3\left(tm\right)\end{cases}}\)
Với t=3 ta có:\(2\sqrt{x+2}+\sqrt{4x+1}=3\)giải ra ta được \(x=\frac{-2}{9}\left(tm\right)\)
Vậy pt có 1 nghiệm duy nhất \(x=-\frac{2}{9}\)

a: Ta có: \(\sqrt{4x+20}-3\sqrt{x+5}+\dfrac{4}{3}\sqrt{9x+45}=6\)
\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
\(\Leftrightarrow x+5=4\)
hay x=-1
b: Ta có: \(\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9x-9}+24\sqrt{\dfrac{x-1}{64}}=-17\)
\(\Leftrightarrow\dfrac{1}{2}\sqrt{x-1}-\dfrac{9}{2}\sqrt{x-1}+3\sqrt{x-1}=-17\)
\(\Leftrightarrow\sqrt{x-1}=17\)
\(\Leftrightarrow x-1=289\)
hay x=290

dk \(x\ge0;2x+1\ge0< =>x\ge0\)
2(x+1)\(\sqrt{x}+\sqrt{3\left(x+1\right)^2\left(2x+1\right)}=\left(x+1\right)\left(5x^2-8x+8\right)< =>\)
\(2\sqrt{x}+\sqrt{3\left(2x+1\right)}=5x^2-8x+8\)(x+1>0 với x\(\ge0\)) <=>
2\(\sqrt{x}-2+\sqrt{6x+3}-3=5x^2-8x+3\) <=>\(\frac{2\left(x-1\right)}{\sqrt{x}+1}+\frac{6\left(x-1\right)}{\sqrt{6x+3}+3}=\left(x-1\right)\left(5x-3\right)< =>\)x-1=0 <=>x= 1 hoặc
\(\frac{2}{\sqrt{x}+1}+\frac{6}{\sqrt{6x+3}+3}=5x-3\)
x>1 thì \(\frac{2}{\sqrt{x}+1}+\frac{6}{\sqrt{6x+3}+3}< \frac{2}{1+1}+\frac{6}{3+3}=2\) hay 5x- 3<2 <=> x<1( vô lý)
x<1 thì \(\frac{2}{\sqrt{x}+1}+\frac{6}{\sqrt{6x+3}+}>2\) hay 5x-3>2 <=> x>1 (vô lý)
x=1 thỏa mãn
vậy pt có nghiệm duy nhất x=1
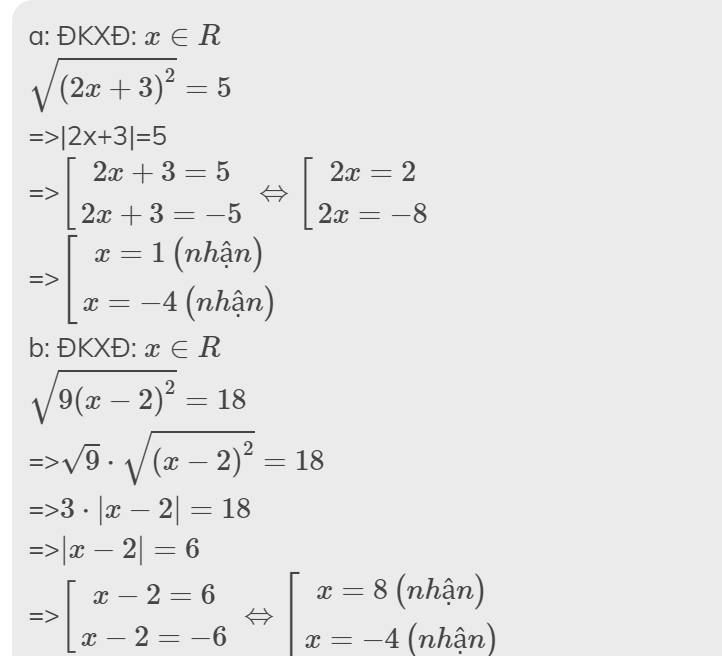
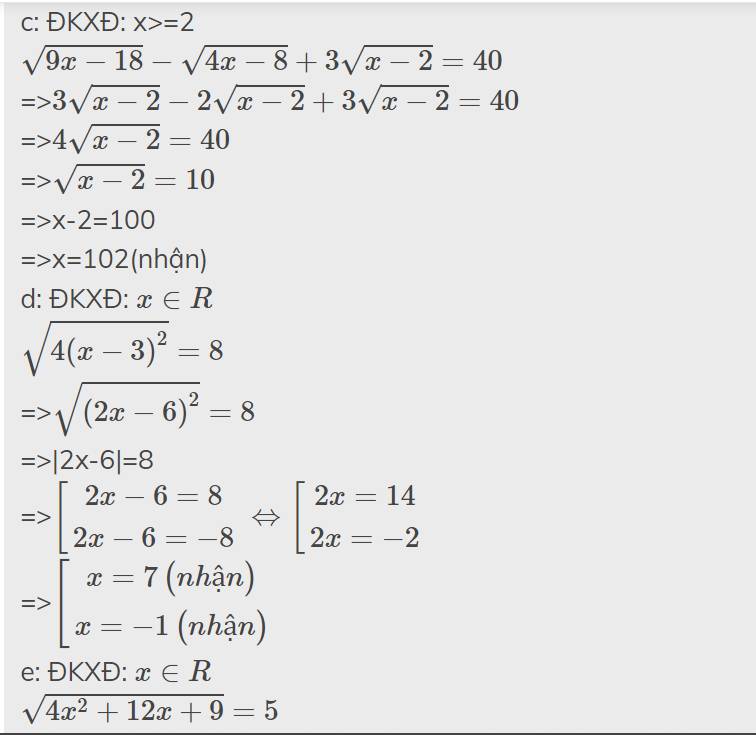
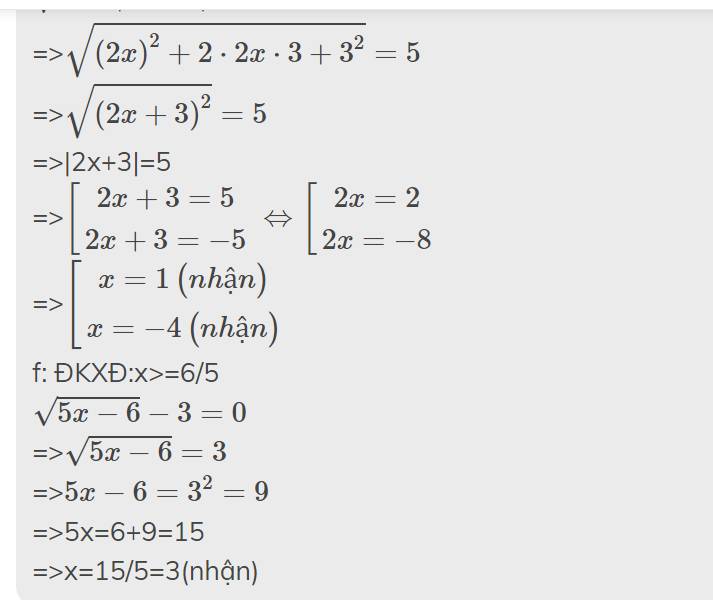
mk làm mất tờ đấy r k chụp lại đc hihi