K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
29 tháng 1 2018
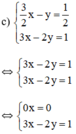
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng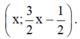 
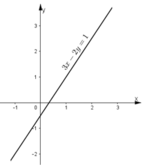
KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm
PK
2
MH
16 tháng 1 2022
\(\left\{{}\begin{matrix}2x-2y=-4\\x+2y=-1\end{matrix}\right.\)
⇒ \(3x=-5\)
⇒ \(x=-\dfrac{5}{3}\)
16 tháng 1 2022
\(a,\left\{{}\begin{matrix}2x-2y=-4\\x+2y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-2y+x+2y=\left(-4\right)+\left(-1\right)\\x+2y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=-5\\x+2y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{3}\\-\dfrac{5}{3}+2y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{3}\\2y=\dfrac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
\(b,\left\{{}\begin{matrix}3x+5y=11\\2x+5y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+5y=11\\3x+5y-2x-5y=11-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3.2+5y=11\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6+5y=11\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=5\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
TH
2
PL
17 tháng 2 2021
\(\hept{\begin{cases}x-\frac{12}{4}=y-\frac{9}{3}=z-1\left(1\right)\\3x+5y-z=2\left(2\right)\end{cases}}\)
từ (1), ta có: \(x-\frac{12}{4}=y-\frac{9}{3}\Rightarrow y=x-\frac{12}{4}+\frac{9}{3}=x\Rightarrow y=x\)
lại có: \(x-\frac{12}{4}=z-1\Rightarrow z=x-\frac{12}{4}+1=x-2\Rightarrow z=x-2\)
từ (2), ta rút y, z theo x, ta được: \(3x+5x-x+2=2\Rightarrow7x=0\Rightarrow x=y=0\)
\(\Rightarrow z=x-2=0-2=-2\)
vậy (x;y;z)=(0;0;-2)
11 tháng 11 2016
Thì phương trình thứ 2 các hệ số của x, y đều gấp 2 lần pt 1 mà VP phương trình 2 không gấp đôi VT pt 1 nên vô nghiệm chớ sao
11 tháng 11 2016
Cả 2 chữ đều là VP hết nha. Viết láu táu nên ghi nhầm thành VT. Sorry nhá
NT
2
11 tháng 4 2022
\(\left\{{}\begin{matrix}4x+5y=9\\2x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=9\\10x-5y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14x=14\\4x+5y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\4.1+5y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
YY
0