Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(sin\left(2x+\frac{\pi}{2}+2\pi\right)-3cos\left(x+\frac{\pi}{2}-4\pi\right)=1+2sinx\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{2}\right)-3cos\left(x+\frac{\pi}{2}\right)=1+2sinx\)
\(\Leftrightarrow cos2x+3sinx=1+2sinx\)
\(\Leftrightarrow1-2sin^2x+sinx=1\)
\(\Leftrightarrow sinx\left(1-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Nghiệm lớn nhất là \(x=\pi\)

1.D
sin2x - 3cosx - 4 = 0
1-cos2x - 3cosx - 4 = 0
cos2x + 3 cosx + 3 = 0
Vô nghiệm

\(\Leftrightarrow sin\left(2x+\frac{\pi}{2}+4\pi\right)-3cos\left(x+\frac{\pi}{2}-8\pi\right)=1+2sinx\)
\(\Leftrightarrow cos2x+3sinx=1+2sinx\)
\(\Leftrightarrow1-2sin^2x+sinx=1\)
\(\Leftrightarrow sinx\left(1-2sinx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\sinx=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\) \(\Rightarrow x=\left\{0;\pi;2\pi;\frac{\pi}{6};\frac{5\pi}{6}\right\}\)
Có 5 nghiệm

\(\cos5x=-\sin4x\)
<=> \(\cos5x=\cos\left(4x+\frac{\pi}{2}\right)\)
\(\Leftrightarrow\orbr{\begin{cases}5x=4x+\frac{\pi}{2}+k2\pi\\5x=-4x-\frac{\pi}{2}+k2\pi\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}}\)
Nghiệm âm lớn nhất: \(-\frac{\pi}{18}\)
Nghiệm dương nhỏ nhất: \(\frac{\pi}{2}\)
pt <=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x-\frac{\pi}{3}+\frac{\pi}{2}\right)\)
<=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x+\frac{\pi}{6}\right)\)
<=> \(\orbr{\begin{cases}5x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\5x+\frac{\pi}{3}=\pi-2x-\frac{\pi}{6}+k2\pi\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{\pi}{18}+\frac{k2\pi}{3}\\x=\frac{\pi}{14}+\frac{k2\pi}{7}\end{cases}}\)
Trên \(\left[0,\pi\right]\)có các nghiệm:
\(\frac{11\pi}{18},\frac{\pi}{14},\frac{5\pi}{14},\frac{9\pi}{14},\frac{13\pi}{14}\)
tính tổng:...


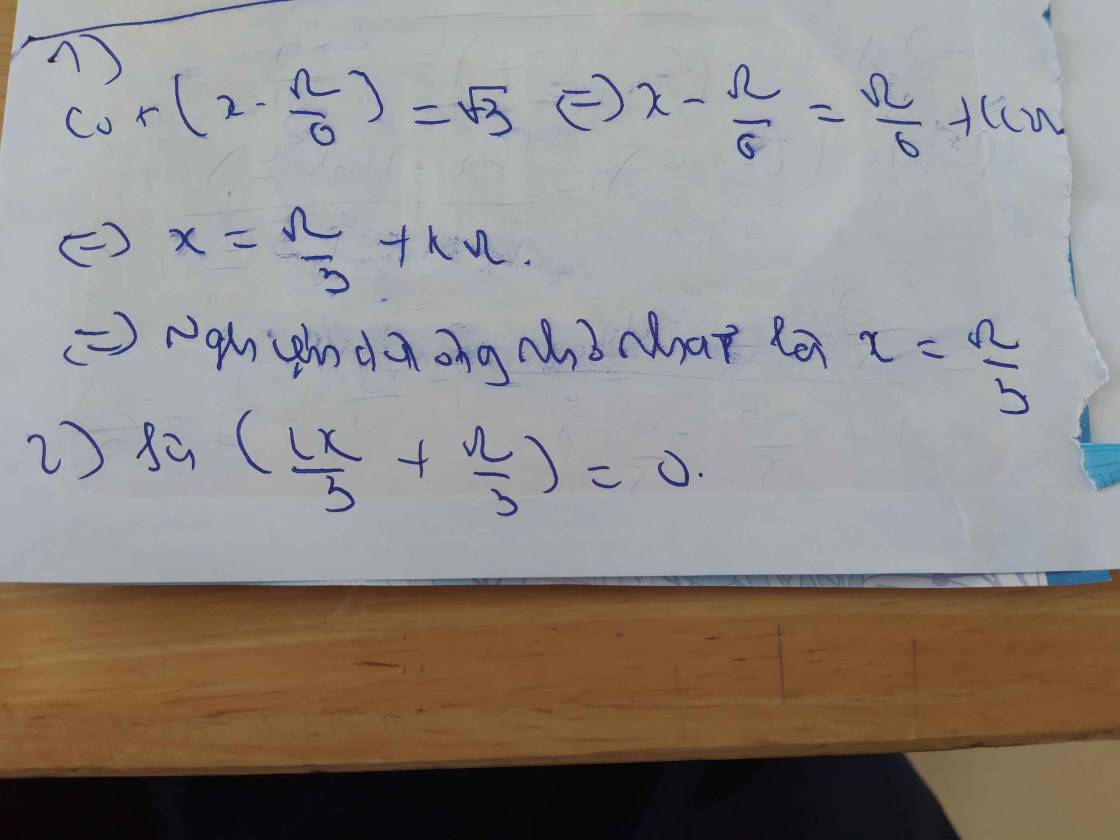

\(3cosx+3sin\left(x+\dfrac{\pi}{7}\right)=0\)
\(\Leftrightarrow cosx+cos\left(\dfrac{5\pi}{14}-x\right)=0\)
\(\Leftrightarrow2cos\dfrac{5\pi}{28}.cos\left(x-\dfrac{5\pi}{28}\right)=0\)
\(\Leftrightarrow cos\left(x-\dfrac{5\pi}{28}\right)=0\)
\(\Leftrightarrow x-\dfrac{5\pi}{28}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{19\pi}{28}+k\pi\)