Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

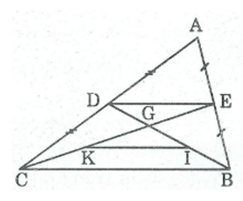
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau tại G gọi I và K theo thứ tự là trung điểm của GB GC
a tứ giác BIKC lF hình gì ? Vì sao?
b tú giác EDKI là hình gì ? Vì sao?

* Trong ΔABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ΔABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ΔGBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ΔGBC⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.

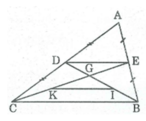
* Trong ∆ ABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ∆ ABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ∆ GBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.

Xét \(\Delta ABC\) có :
\(AE=EB\left(gt\right)\)
\(AD=DC\left(gt\right)\)
\(\Rightarrow ED\) là đường trung bình
\(\Rightarrow ED\)//\(BC\) và \(ED=\frac{1}{2}BC\) ( 1 )
Xét \(\Delta GBC\) có :
\(GI=IB\left(gt\right)\)
\(GK=KC\left(gt\right)\)
\(\Rightarrow IG\) là đường trung bình
\(\Rightarrow IG\)//\(BC\) và \(IG=\frac{1}{2}BC\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow DE\)//\(IK\) và \(DE\)=\(IK\)
A E B D C I G K
+) Tam giác ABC có D; E là trung điểm của AB; AC
=> DE là đường tring bình của tam giác => DE// BC và DE = BC/2 (1)
+) Tam giác GBC có I: K là Trung điểm của GB; GC
=> IK là đường trung bình của tam giác
=> IK //BC và IK = BC/ 2 (2)
Từ (1)(2) => DE//IK và DE = IK

Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(1)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra DE//IK và DE=IK

dễ thấy DE là đường trung bình tam giác ABC nên BEDC là hình thang, lại có BM=MC,DN=NC=> MN là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì . Lại có .Từ (1)(2) => Q.E.
bạn tham khảo nha

tim mot so tu nhien 6 chu so biet rang chu so neu chuyen chu so hang don vi la 4 va neu chuyen chu so do nen hang dau tien thi so do tang gap 4 lan