Giải hệ PT \(\left\{{}\begin{matrix}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y\sq...

K

Khách

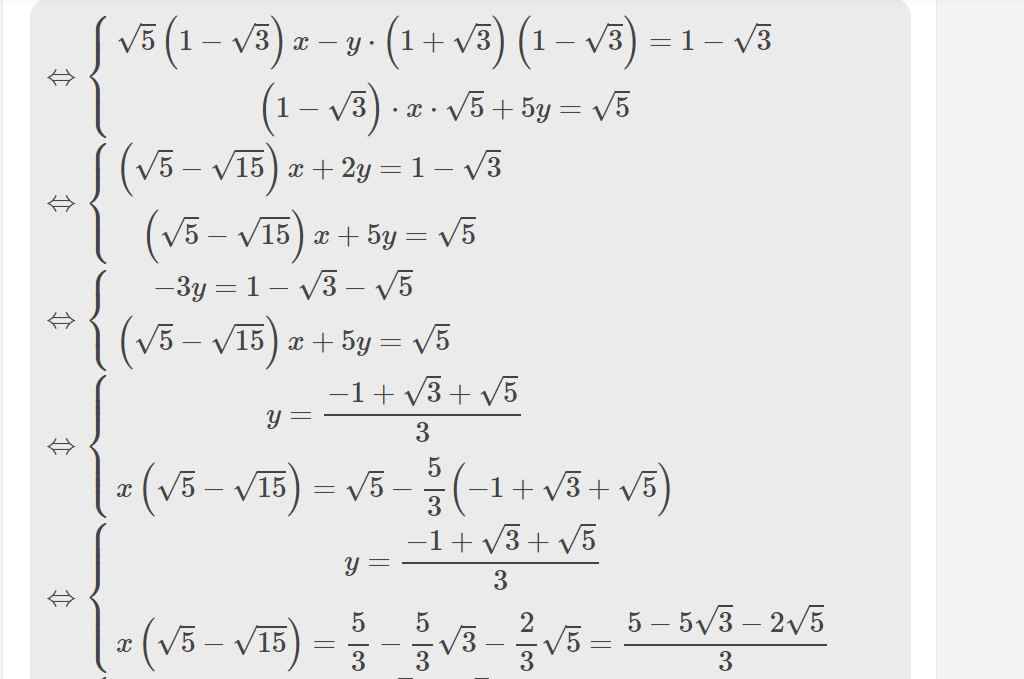
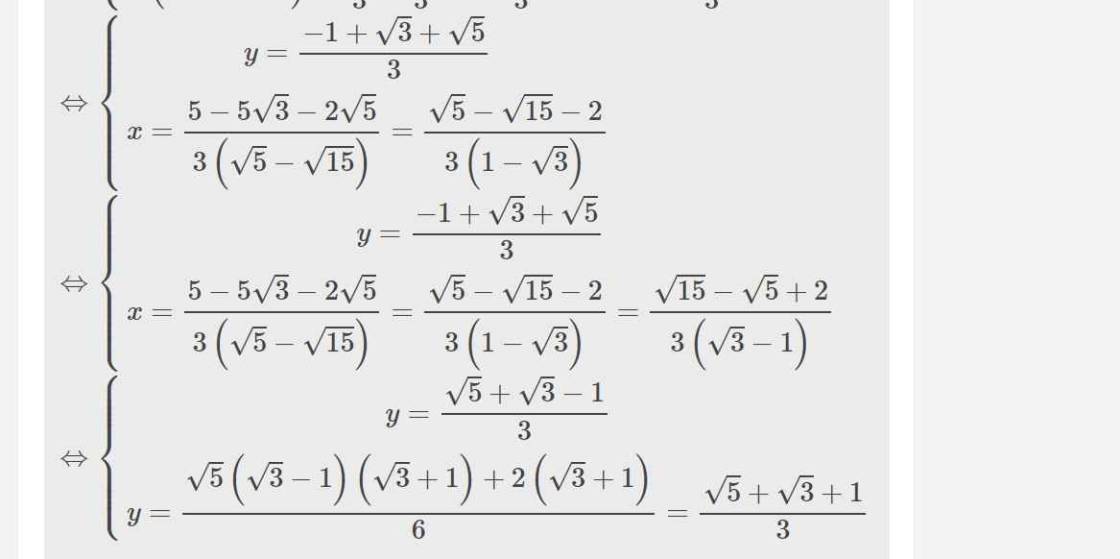
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

N

Na

16 tháng 1 2019

Giải hệ PT

\(\left\{{}\begin{matrix}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{matrix}\right.\)

2

TS

Thời Sênh

12 tháng 1 2019

https://i.imgur.com/RKDsxW4.jpg

NL

Nguyễn Lê Phước Thịnh

1 tháng 1 2023

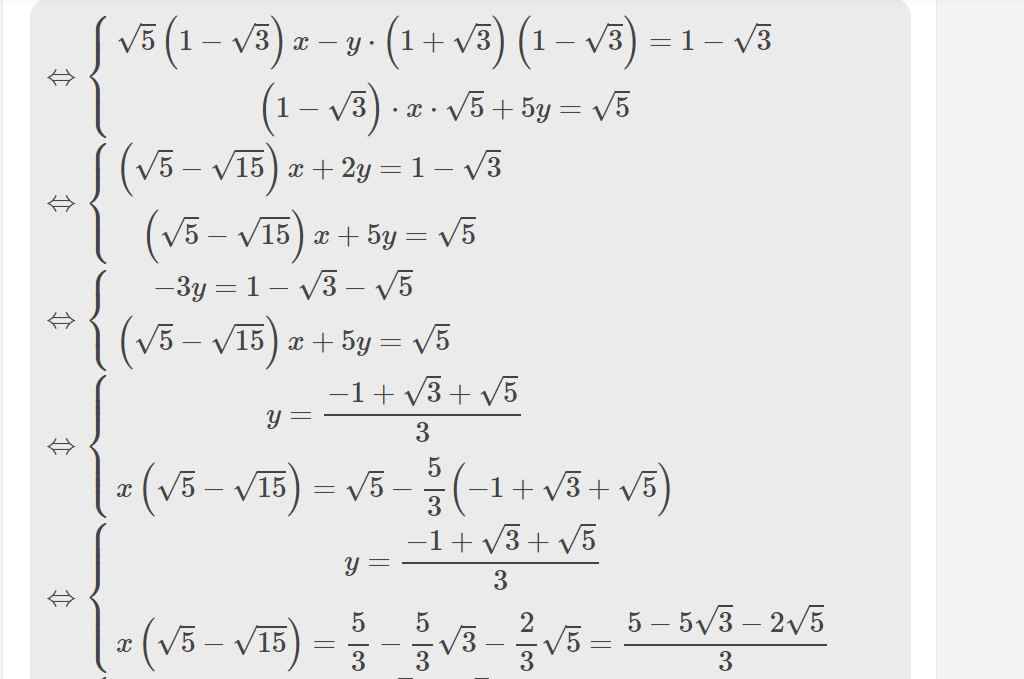
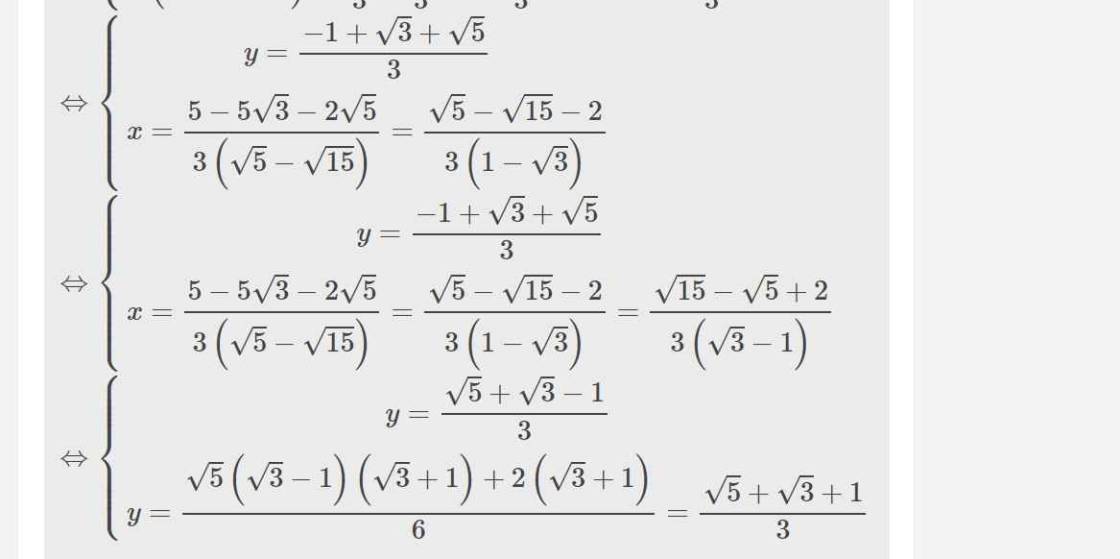
loading...

loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

N

Na

16 tháng 1 2019

Giải hệ PT:

\(\left\{{}\begin{matrix}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{matrix}\right.\)

1

NL

Nguyễn Lê Phước Thịnh

1 tháng 1 2023

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{5}\left(1-\sqrt{3}\right)x-y\cdot\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)=1-\sqrt{3}\\\left(1-\sqrt{3}\right)\cdot x\cdot\sqrt{5}+5y=\sqrt{5}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{5}-\sqrt{15}\right)x+2y=1-\sqrt{3}\\\left(\sqrt{5}-\sqrt{15}\right)x+5y=\sqrt{5}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-3y=1-\sqrt{3}-\sqrt{5}\\\left(\sqrt{5}-\sqrt{15}\right)x+5y=\sqrt{5}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x\left(\sqrt{5}-\sqrt{15}\right)=\sqrt{5}-\dfrac{5}{3}\left(-1+\sqrt{3}+\sqrt{5}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x\left(\sqrt{5}-\sqrt{15}\right)=\dfrac{5}{3}-\dfrac{5}{3}\sqrt{3}-\dfrac{2}{3}\sqrt{5}=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3\left(\sqrt{5}-\sqrt{15}\right)}=\dfrac{\sqrt{5}-\sqrt{15}-2}{3\left(1-\sqrt{3}\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1+\sqrt{3}+\sqrt{5}}{3}\\x=\dfrac{5-5\sqrt{3}-2\sqrt{5}}{3\left(\sqrt{5}-\sqrt{15}\right)}=\dfrac{\sqrt{5}-\sqrt{15}-2}{3\left(1-\sqrt{3}\right)}=\dfrac{\sqrt{15}-\sqrt{5}+2}{3\left(\sqrt{3}-1\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{5}+\sqrt{3}-1}{3}\\y=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)+2\left(\sqrt{3}+1\right)}{6}=\dfrac{\sqrt{5}+\sqrt{3}+1}{3}\end{matrix}\right.\)

N

Na

16 tháng 1 2019

Giải hệ PT:

\(\left\{{}\begin{matrix}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{matrix}\right.\)

2

N

Na

17 tháng 1 2019

Mysterious Person Nguyễn Huy Thắng Hung nguyen help. Thanks!!

NL

Nguyễn Lê Phước Thịnh

1 tháng 1 2023

loading...

loading...

LD

Lê Dương

4 tháng 3 2020

\(\left\{{}\begin{matrix}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{matrix}\right.\)

giải hệ pt

1

NT

nguyễn thị mai linh

11 tháng 3 2020

Hệ hai phương trình bậc nhất hai ẩn

G

G.Dr

9 tháng 2 2020

giải các hệ pt sau:

a) \(\left\{{}\begin{matrix}x+2y=-1\\x-y=5\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}\frac{5}{x}-\frac{6}{y}=3\\\frac{4}{x}+\frac{9}{y}=7\end{matrix}\right.\)

c) \(\left\{{}\begin{matrix}3\sqrt{x+1}+\sqrt{y-1}=1\\\sqrt{x+1}-\sqrt{y-1}=-2\end{matrix}\right.\)

d) \(\left\{{}\begin{matrix}\left|x-1\right|+y=5\\4x+3y=23\end{matrix}\right.\)

1

PM

Phạm Minh Quang

9 tháng 2 2020

a) \(\left\{{}\begin{matrix}x+2y=-1\\x-y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3y=-6\\x-y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=3\end{matrix}\right.\)

Vậy..............................................................................

b) \(\left\{{}\begin{matrix}\frac{5}{x}-\frac{6}{y}=3\\\frac{4}{x}+\frac{9}{y}=7\end{matrix}\right.\)ĐKXĐ: x,y≠0

\(\Leftrightarrow\left\{{}\begin{matrix}\frac{20}{x}-\frac{24}{y}=12\\\frac{20}{x}+\frac{45}{y}=35\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\frac{69}{y}=23\\\frac{20}{x}+\frac{45}{y}=35\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=10\end{matrix}\right.\)

Vậy...................................................................................

c) \(\left\{{}\begin{matrix}3\sqrt{x+1}+\sqrt{y-1}=1\\\sqrt{x+1}-\sqrt{y-1}=-2\end{matrix}\right.\)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge-1\\y\ge1\end{matrix}\right.\)

\(\Rightarrow4\sqrt{x+1}\)\(=-1\)(vô nghiệm)

Vậy hệ pt vô nghiệm

d) Nhân 3 pt đầu rồi thu gọn

TN

Thanh Nguyễn

6 tháng 1 2019

Giải hệ pt:

a)\(\left\{{}\begin{matrix}x-\left(1+\sqrt{3}\right)y=1\\\left(1-\sqrt{3}\right)x+y=1\end{matrix}\right.\)

b)\(\left\{{}\begin{matrix}-x-\sqrt{2}y=\sqrt{3}\\\sqrt{2}x+2y=-\sqrt{6}\end{matrix}\right.\)

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 12 2022

a: \(\Leftrightarrow\left\{{}\begin{matrix}\left(1-\sqrt{3}\right)x+2y=1-\sqrt{3}\\\left(1-\sqrt{3}\right)x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\sqrt{3}\\x=1+\left(1+\sqrt{3}\right)\cdot\left(-\sqrt{3}\right)=-2-\sqrt{3}\end{matrix}\right.\)

b: \(\Leftrightarrow\left\{{}\begin{matrix}-x-\sqrt{2}y=\sqrt{3}\\x+\sqrt{2}y=-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in R\\x=-\sqrt{3}-y\sqrt{2}\end{matrix}\right.\)

TN

Thanh Nguyễn

19 tháng 1 2019

Giải hệ pt

\(\left\{{}\begin{matrix}2\left|x-1\right|+\sqrt{y-1}=5\\\left|x-1\right|+\sqrt{y-1}=3\end{matrix}\right.\)

2

QT

Quang Thuý

23 tháng 1 2019

Đặt trị tuyệt đối x-1 = a

căn y-1 =b

thay vào hệ :

2a+b=5

a+b=3

có nghiêm(2;1)

Suy ra: trị tuyệt đối x-1=2

<=> x=3 hoặc x=x=-1

căn y-1 =1

<=> y=2

Sorry nha..phần gõ công thức mình bị lỗi nên k gõ được rõ cho lắm

DD

đào danh phước

21 tháng 1 2020

theo bài ra ta có

\(|x-1|=2\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)

thay vào phương trình thứ 2

với x=3

\(\Leftrightarrow2+\sqrt{y-1}=3\\ \Leftrightarrow\sqrt{y-1}=1\\ \Leftrightarrow y=2\)

với x=-1

\(\Leftrightarrow2+\sqrt{y-1}=3\\ \Leftrightarrow\sqrt{y-1}=1\\ \Leftrightarrow y=2\)

vậy (x,y)=(3,2)=(-1,2)

TT

Trần Thu Trang

22 tháng 2 2018

giải hệ pt:

(1)\(\left\{{}\begin{matrix}2\text{x}+2y+2\text{x}y=10\\x^2+y^2=5\end{matrix}\right.\)

(2)\(\left\{{}\begin{matrix}\sqrt{x}+\sqrt{y}=3\\\sqrt{xy}=2\end{matrix}\right.\)

(3)\(\left\{{}\begin{matrix}x-y=1\\x.y=6\end{matrix}\right.\)

(4)\(\left\{{}\begin{matrix}|x|+y=3\\2|x|-y=3\end{matrix}\right.\)

1

DV

Đàm Vũ Đức Anh

24 tháng 2 2018

Câu 1 \(\left\{{}\begin{matrix}2x+2y+2xy=10\left(1\right)\\x^2+y^2=5\left(2\right)\end{matrix}\right.\)

=>2.(2) - (1)=\(\left(x-1\right)^2+\left(y-1\right)^2+\left(x-y\right)^2=0\)

<=>\(\left\{{}\begin{matrix}x-1=0\\y-1=0\\x-y=0\end{matrix}\right.\) =>x=y=1

Câu 2 dùng vi-et đảo

Câu 3 rút x=y+1 từ pt trên rồi thế xuống dưới

Câu 4 lấy pt trên cộng pt dưới rồi xét dấu GTTĐ

ML

Mỹ Lệ

19 tháng 2 2018

0

KT

Kim Trí Ngân

24 tháng 2 2019

Giải hệ phương trình: 1. \(\left\{{}\begin{matrix}x+3=2\sqrt{\left(3y-x\right)\left(y+1\right)}\\\sqrt{3y-2}-\sqrt{\dfrac{x+5}{2}}=xy-2y-2\end{matrix}\right.\) 2. \(\left\{{}\begin{matrix}\sqrt{2y^2-7y+10-x\left(y+3\right)}+\sqrt{y+1}=x+1\\\sqrt{y+1}+\dfrac{3}{x+1}=x+2y\end{matrix}\right.\) 3. \(\left\{{}\begin{matrix}\sqrt{4x-y}-\sqrt{3y-4x}=1\\2\sqrt{3y-4x}+y\left(5x-y\right)=x\left(4x+y\right)-1\end{matrix}\right.\) 4....

0