
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Với m=2 thì hpt trở thành:
x-2y=5
2x-y=7
<=>
2x-4y=10
2x-y=7
<=>
-3y=3
2x-y=7
<=>
y=-1
x=3
b)\(\int^{\left(m-1\right)x-my=3m-1}_{2x-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{\frac{6m+2my-2}{m-1}-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{m^2+2m+my+y+3=0}\)
*m2+2m+my+y+3=0
<=>y.(m+1)=-m2-2m-3
*Với m=-1 =>PT vô nghiệm
*Với m khác -1 =>PT có nghiệm là: \(y=\frac{-m^2-2m-3}{m+1}=-m-1-\frac{2}{m+1}\)
bí tiếp

Câu này dễ mà, sao c lm CTV được:vv
\(\hept{\begin{cases}2x^2+\frac{x}{2x-y}=2\left(1\right)\\y^2+\frac{y}{2x-y}=4\left(2\right)\end{cases}}\)
ĐKXĐ: \(2x-y\ne0\)
Nhân 2 vế PT (1) với 2 rồi trừ đi PT (2) ta được:
\(4x^2-y^2+1=0\left(3\right)\)
Ta xét 2 trường hợp:
TH1:\(2x+y=0\)<=>\(y=-2x\)
Thay vào PT (1) rồi ta tính được \(\left(x;y\right)=\left(\pm\sqrt{\frac{7}{8}};\mp2\sqrt{\frac{7}{8}}\right)\)
TH2: \(2x+y\ne0\)
<=>\(2x-y=\frac{-1}{2x+y}\)
Thay vào PT(1) ta được:
\(xy=-2\)
Thay vào \(4x^2-y^2+1=0\)ta tính được
\(\left(x;y\right)=\left(...\right)\)
Vậy....
Phần tính toán cậu tự tính nhé:vvv
@Lê Phúc Huy: lí do mik đã viết thẳng vào câu hỏi. Ngay dòng dòng đầu mà bạn không thấy à. Hay mắt lé mà không thấy :]>

Với m =1 suy ra :
\(\hept{\begin{cases}2x-y=1\\-x+y=2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=2x-1\\-x+2x-1=2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=2.3-1=5\\x=3\end{cases}}\)
b ) Để hệ có nghiệm x+2y=3
\(\Rightarrow\hept{\begin{cases}x+2y=3\\-x+y=2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=3-2y\\-\left(3-2y\right)+y=2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=3-2.\frac{5}{3}=-\frac{1}{3}\\y=\frac{5}{3}\end{cases}}\)
\(\Rightarrow2.\left(-\frac{1}{3}\right)-\frac{5}{3}=2m-1\Rightarrow m=-\frac{2}{3}\)

Hệ có nghiệm duy nhất khi và chỉ khi \(\frac{m-1}{2}\ne\frac{-m}{-1}\Leftrightarrow m\ne-1\)
Xét m=0 thì x=1, y=-3 --> thỏa mãn
Xét m khác 0 thì nhân 2 vế của đẳng thức thứ 2 cho m ---> \(\hept{\begin{cases}\left(m-1\right)x-my=3m-1\\2mx-my=m^2+5m\end{cases}}\)
Lấy đẳng thức 2 trừ đẳng thức 1 vế theo vế--> Dễ dàng tính được x=m+1, y=m-3 ---> thế vào điều kiện:
\(x^2-y^2< 4\Leftrightarrow\left(m+1\right)^2-\left(m-3\right)^2< 4\Leftrightarrow8m-8< 4\Leftrightarrow m< \frac{3}{2}\)
Đối chiếu điều kiện có nghiệm duy nhất---> Kết luận \(m< \frac{3}{2},m\ne-1\)

a) \(\hept{\begin{cases}2x+my=5\\3x-y=0\end{cases}\left(1\right)}\)
Thay m=0 vào (1) \(\Rightarrow\hept{\begin{cases}2x=5\\3x-y=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\\frac{5}{2}\cdot3=y\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{15}{2}\end{cases}}}\)

Ta có: \(\hept{\begin{cases}\left(\frac{1}{x}+y\right)+\left(\frac{1}{x}-y\right)=\frac{5}{8}\\\left(\frac{1}{x}+y\right)-\left(\frac{1}{x}-y\right)=-\frac{3}{8}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2}{x}=\frac{5}{8}\\2y=-\frac{3}{8}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{16}{5}\\y=-\frac{3}{16}\end{cases}}}\)
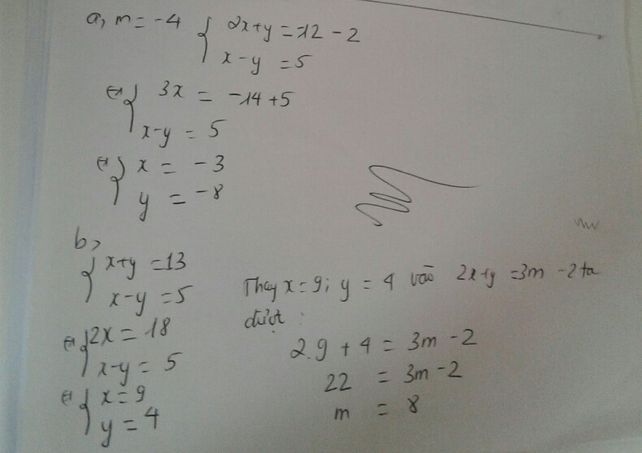 Bn tham khảo nhé!
Bn tham khảo nhé!