K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 9 2016
phương trình \(\left(2\right)\Leftrightarrow y=3x-5\) phương trình ( 3 ) .
\(\left(1\right)\Rightarrow5x+2\left(3x-5\right)=23\)
\(\Leftrightarrow5x+6x-10=23\)
\(\Leftrightarrow11x=33\Leftrightarrow x=3\)
\(\left(3\right)\Rightarrow y=4\). Vậy nghiệm của hệ đã cho là : ( 3 ; 4 )
2 tháng 5 2020
\(\left\{{}\begin{matrix}4x+y=-5\\3x+12=2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+y=-5\\3x-2y=-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-4x-5\\3x-2\left(-4x-5\right)=-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-4x-5\\3x+8x+10=-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-4x-5\\11x=-22\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-4x-5\\x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)
26 tháng 8 2016
a ) \(\begin{cases}3x-y=5\\5x+2y=23\end{cases}\)
Từ phương trình \(\left(1\right)\) \(\Leftrightarrow y=3x-5\) \(\left(3\right)\)
Thế \(\left(3\right)\) vào phương trình \(\left(2\right)\) : \(5x+2\left(3x-5\right)=23\)
\(\Leftrightarrow5x+6x-10=23\Leftrightarrow11x=33\Leftrightarrow x=3\)
Từ đó \(y=3.3-5=4\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(3;4\right)\)
b ) \(\begin{cases}3x+5y=1\\2x-y=-8\end{cases}\)
Từ hệ phương trình \(\left(2\right)\) \(\Leftrightarrow y=3x+8\)
Thế (3) vào (1): \(3x+5\left(2x+8\right)=1\Leftrightarrow3x+10x+40=1\Leftrightarrow13x=-39\)
\(\Leftrightarrow x=-3\)
Từ đó \(y=2\left(-3\right)+8=2\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(-3;2\right)\)
CM
12 tháng 9 2018
Cách 1
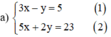
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
24 tháng 12 2019
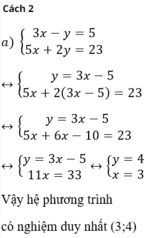
a,Ta có hệ phương trình\(\left\{{}\begin{matrix}7x-2y=1\left(1\right)\\2x+3y=11\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}21x-6y=3\\4x+6y=22\end{matrix}\right.\)
=> \(21x-6y+4x+6y=25\)
=> \(25x=25\)
=> \(x=1\)
- Thay x = 1 vào phương trình 1 ta được :
\(7-2y=1\)
=> \(y=3\)
Vậy hệ phương trình có duy nhất 1 nghiệm là ( x, y ) = ( 1, 3 )
b, Ta có hệ phương trình\(\left\{{}\begin{matrix}3x+2y=16\\2x-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+2y=16\\y=2x+1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3x+2\left(2x+1\right)=16\\y=2x+1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3x+4x+2=16\\y=2x+1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=2\\y=2x+1\end{matrix}\right.\)=> \(\left\{{}\begin{matrix}x=2\\y=2.2+1=5\end{matrix}\right.\)
Vậy hệ phương trình có duy nhất 1 nghiệm là ( x, y ) = ( 2, 5 )
c, Ta có hệ phương trình \(\left\{{}\begin{matrix}x+2y=5\\3x-2y=-1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=5-2y\\3x-2y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=5-2y\\3\left(5-2y\right)-2y=-1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=5-2y\\15-6y-2y=-1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=5-2y\\y=2\end{matrix}\right.\)=> \(\left\{{}\begin{matrix}x=5-2.2=1\\y=2\end{matrix}\right.\)
Vậy hệ phương trình có duy nhất 1 nghiệm là ( x, y ) = ( 1, 2 )
20 tháng 9 2021
\(a,\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\ b,\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\23y=46\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
\(c,\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\ d,\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
\(e,\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
HP
20 tháng 9 2021
a. \(\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x=20\\6x-2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23y=46\\5x+2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\4x+3y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\4x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\5x+2y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=33\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\\15+2y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
\(\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-6x+2y=-10\\5x+2y=23\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\11x=33\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)