NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
0
NV
0
17 tháng 5 2017
\(\hept{\begin{cases}2y^3-x^3=1\\x^5+x^2y^2\left(x-y\right)+xy=2y^5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2y^3-x^3=1\\x^5+x^2y^2\left(x-y\right)+xy\left(2y^3-x^3\right)=2y^5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2y^3-x^3=1\left(1\right)\\x^5+x^3y^2-x^2y^3+2xy^4-x^4y=2y^5\left(2\right)\end{cases}}\)
Xét PT (2) ta có:
\(x^5+x^3y^2-x^2y^3+2xy^4-x^4y=2y^5\)
Dễ thấy y = 0 không phải là nghiệm của hệ
Ta đặt \(x=ty\) thì ta có
\(\left(ty\right)^5+\left(ty\right)^3y^2-\left(ty\right)^2y^3+2tyy^4-\left(ty\right)^4y=2y^5\)
\(\Leftrightarrow t^5-t^4+t^3-t^2+2t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^4+t^2+2\right)=0\)
Vì \(t^4+t^2+2>0\)
\(\Rightarrow t=1\)
\(\Rightarrow x=y\)
Thế vô (1) ta được
\(2x^3-x^3=1\)
\(\Leftrightarrow x=y=1\)
24 tháng 1 2021
a) Ta có: \(\left\{{}\begin{matrix}-x+2y=3\\3x+y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3x+6y=9\\3x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=8\\-x+2y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{8}{7}\\-x=3-2y=3-2\cdot\dfrac{8}{7}=\dfrac{5}{7}\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=-\dfrac{5}{7}\\y=\dfrac{8}{7}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{5}{7}\\y=\dfrac{8}{7}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}2x+2\sqrt{3}\cdot y=1\\\sqrt{3}x+2y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x+6y=\sqrt{3}\\2\sqrt{3}x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2y=\sqrt{3}+10\\\sqrt{3}x+2y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{3}+10}{2}\\x\sqrt{3}+2\cdot\dfrac{\sqrt{3}+10}{2}=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{3}+10}{2}\\x\sqrt{3}=-5-\sqrt{3}-10=-15-\sqrt{3}\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=-1-5\sqrt{3}\\y=\dfrac{\sqrt{3}+10}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-1-5\sqrt{3}\\y=\dfrac{\sqrt{3}+10}{2}\end{matrix}\right.\)
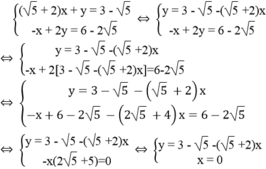
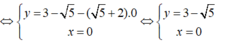
Lời giải:
$2x+|2y-5|=3$
$x-3|2y-5|=-2$
$\Rightarrow 3(2x+|2y-5|)+(x-3|2y-5|)=3.3+(-2)$
$\Leftrightarrow 7x=7$
$\Leftrightarrow x=1$
$|2y-5|=3-2x=3-2.1=1$
$\Rightarrow 2y-5=\pm 1$
$\Rightarrow y=3$ hoặc $y=2$
Vậy $(x,y)=(1,3); (1,2)$