K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Thông cảm mk bị cận!
13 tháng 5 2017
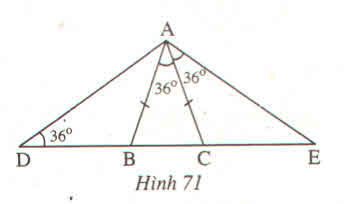
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
28 tháng 7 2017
Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )
H
20 tháng 4 2017
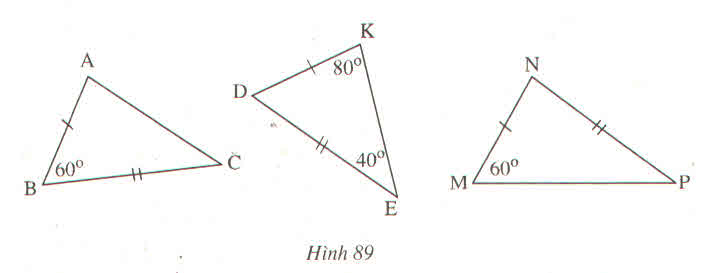
Tam giác DKE có:
\(\widehat{D}+\widehat{K}+\widehat{E}\)=1800 (tổng ba góc trong của tam giác).
\(\widehat{D}\)+800 +400=1800
\(\widehat{D}\)=1800 -1200= \(60^0\)
Nên ∆ ABC và ∆KDE có:
AB=KD(gt)
\(\widehat{B}\)=\(\widehat{D}\)=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại.
Bài 1:
Gọi $d$ là ƯCLN của $a$ và $b$. Khi đó:
$a=dx, b=dy$ với $x,y$ là 2 số nguyên tố cùng nhau.
$p=a+b=dx+dy=d(x+y)$.
Hiển nhiên $x+y\geq 2$ nên nếu $d\geq 2$ thì $p=d(x+y)$ không thể là số nguyên tố (trái giả thiết)
Do đó: $d=1$
Tức là $a,b$ nguyên tố cùng nhau. Ta có đpcm.
Bài 2:
** $a,b$ ở đây là các số tự nhiên.
$a^2-b^2=(a-b)(a+b)$. Để $a^2-b^2$ là SNT thì 1 trong 2 thừa số $a-b, a+b$ phải bằng $1$ và số còn lại là SNT.
Mà: $a-b< a+b$ với $a,b\in\mathbb{N}$ nên $a-b=1$
$\Rightarrow a+b=a^2-b^2$