Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét ∆ ABC vuông tại A
➡️AB2 + AC2 = BC2 (Pitago)
➡️BC2 = 32 + 42
➡️BC2 = 25
➡️BC = 5 (cm)
b, Xét ∆ ABD và ∆ EBD có:
Góc A = góc E = 90°
BD chung
Góc ABD = góc EBD (gt)
➡️∆ ABD = ∆ EBD (ch - gn)
➡️AB = EB (2 cạnh t/ư)
c, Ta có:
BA + AK = BK
BE + EC = BC
mà AB = EB (cmt)
AK = EC (gt)
➡️BK = BC
Xét ∆ BKI và ∆ BCI có:
BK = BC (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ BKI = ∆ BCI (c.g.c)
➡️Góc BKI = góc BCI (2 góc t/ư)
d, Xét ∆ ABI và ∆ EBI có:
AB = EB (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ ABI = ∆ EBI (c.g.c)
➡️IA = IE (2 cạnh t/ư)
Hok tốt~

bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI

Xin lỗi mk ko biết vẽ hình trên máy
a) Xét tam giác ABD và tan giác EBD có :
BD chung
góc ABD = góc EBD ( vì BD la phân giác góc B )
góc A = góc E ( = 90 )
=> Tam giác ABD = tam giác EBD ( cạnh huyền- góc nhọn )
=> AD = DE
Chúc bạn hc tốt

a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E
có: góc ABD = góc EBD (gt)
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)\)
b) Xét tam giác ABC vuông tại A
có: \(AB^2+AC^2=BC^2\) ( py - ta - go)
thay số: \(6^2+8^2=BC^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10cm\)
ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AB = EB = 6cm ( 2 cạnh tương ứng)
=> EB = 6cm
mà EB + EC = BC ( E thuộc BC )
thay sô: 6 cm + EC = 10 cm
EC = 10 cm - 6 cm
EC = 4 cm
c) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AD = ED ( 2 cạnh tương ứng)
Xét tam giác ADI vuông tại A và tam giác EDC vuông tại E
có: góc ADI = góc EDC ( đối đỉnh)
AD = ED ( cmt)
\(\Rightarrow\Delta ADI=\Delta EDC\left(cgv-gn\right)\)
=> AI = EC ( 2 cạnh tương ứng)
Mà AB = BE ( tam giác ABD = tam giác EBD)
=> AI + AB = EC + BE
=> IB = CB
=> tam giác BIC cân tại B ( định lí tam giác cân)
d) ta có: AD = ED ( tam giác ABD = tam giác EBD) (1)
Xét tam giác EDC vuông tại E
có: ED < DC ( định lí cạnh huyền, góc nhọn) (2)
Từ (1); (2) => AD < DC
xin lỗi bn nha! mk ko bít kẻ hình trên này, nên mk ko kẻ cho bn đc đâu
a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E
có: góc ABD = góc EBD (gt)
BD là cạnh chung
⇒ΔABD=ΔEBD(ch−gn)⇒Δ���=Δ���(�ℎ−��)
b) Xét tam giác ABC vuông tại A
có: AB2+AC2=BC2��2+��2=��2 ( py - ta - go)
thay số: 62+82=BC262+82=��2
⇒BC2=100⇒��2=100
⇒BC=10cm⇒��=10��
ta có: ΔABD=ΔEBD(pa)Δ���=Δ���(��)
=> AB = EB = 6cm ( 2 cạnh tương ứng)
=> EB = 6cm
mà EB + EC = BC ( E thuộc BC )
thay sô: 6 cm + EC = 10 cm
EC = 10 cm - 6 cm
EC = 4 cm
c) ta có: ΔABD=ΔEBD(pa)Δ���=Δ���(��)
=> AD = ED ( 2 cạnh tương ứng)
Xét tam giác ADI vuông tại A và tam giác EDC vuông tại E
có: góc ADI = góc EDC ( đối đỉnh)
AD = ED ( cmt)
⇒ΔADI=ΔEDC(cgv−gn)⇒Δ���=Δ���(���−��)
=> AI = EC ( 2 cạnh tương ứng)
Mà AB = BE ( tam giác ABD = tam giác EBD)
=> AI + AB = EC + BE
=> IB = CB
=> tam giác BIC cân tại B ( định lí tam giác cân)
d) ta có: AD = ED ( tam giác ABD = tam giác EBD) (a)
Xét tam giác EDC vuông tại E
có: ED < DC ( định lí cạnh huyền, góc nhọn) (b)
Từ (a); (b) => AD < DC.
cre baji
![]()
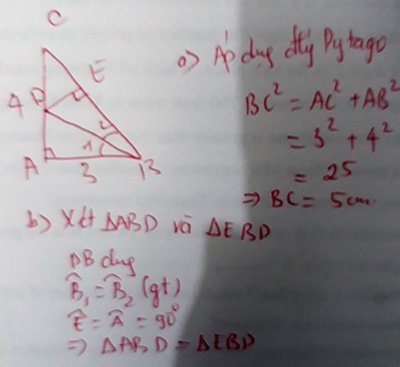
d: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>góc BKC=góc BCK