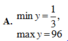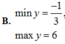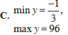Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)

a)\(y=\sqrt{3}sinx+cosx=2\left(\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx\right)\)\(=2\left(sinx.cos\dfrac{\pi}{6}+cosx.sin\dfrac{\pi}{6}\right)\)\(=2sin\left(x+\dfrac{\pi}{6}\right)\)
Có \(-1\le sin\left(x+\dfrac{\pi}{6}\right)\le1\) \(\Leftrightarrow-2\le2sin\left(x+\dfrac{\pi}{6}\right)\le2\)
\(\Leftrightarrow-2\le y\le2\)
miny=-2 \(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=-1\) \(\Leftrightarrow x+\dfrac{\pi}{6}=-\dfrac{\pi}{2}+2k\pi\left(k\in Z\right)\) \(\Leftrightarrow x=-\dfrac{2\pi}{3}+k2\pi\left(k\in Z\right)\)
maxy=2\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=1\) \(\Leftrightarrow x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)\(\Leftrightarrow x=\dfrac{\pi}{3}+k2\pi\left(k\in Z\right)\)
b) \(y=sin2x-cos2x=\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)\)
Có \(\sqrt{2}\ge\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)\ge-\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}\ge y\ge-\sqrt{2}\)
miny=\(-\sqrt{2}\) \(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=-1\)\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\left(k\in Z\right)\)
maxy=\(\sqrt{2}\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=1\)\(\Leftrightarrow x=\dfrac{3\pi}{8}+k\pi\left(k\in Z\right)\)
c) \(y=3sinx+4cosx=5\left(\dfrac{3}{5}sinx+\dfrac{4}{5}cosx\right)\)
Đặt \(cosa=\dfrac{3}{5}\) và \(sina=\dfrac{4}{5}\)(vì cos2a+sin2a=1)
\(y=5\left(sinx.cosa+cosx.sina\right)\)\(=5sin\left(x+a\right)\)
\(\Rightarrow-5\le y\le5\)
miny=-5 <=> \(sin\left(x+a\right)=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}-arc.sina+k2\pi\left(k\in Z\right)\)
maxy=5 <=> \(sin\left(x+a\right)=1\)\(\Leftrightarrow x=\dfrac{\pi}{2}-arc.sina+k2\pi\left(k\in Z\right)\)
(P/s1:cái x ở câu c ấy trông nó ngu ngu??
P/s2:sau khi load lại câu hỏi ở 1 tab khác ,thấy 1 câu trả lời nhưng vẫn đăng vì cảm thấy bỏ đi hơi phí :?)
Áp dụng quy tắc sau: Nếu \(a\sin x+b\cos y=c\Leftrightarrow a^2+b^2\ge c^2\)
a/ \(3+1\ge y^2\Leftrightarrow4\ge y^2\Leftrightarrow-2\le y\le2\)
\(y_{max}=2\Leftrightarrow\sqrt{3}\sin x+\cos x=2\Leftrightarrow\dfrac{\sqrt{3}}{2}\sin x+\dfrac{1}{2}\cos x=1\Leftrightarrow\cos\dfrac{\pi}{6}.\sin x+\sin\dfrac{\pi}{6}.\cos x=1\)
\(\Rightarrow\sin\left(x+\dfrac{\pi}{6}\right)=1\Leftrightarrow x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\Leftrightarrow x=\dfrac{\pi}{3}+k2\pi\)
\(y_{min}=-2\Leftrightarrow\sin\left(x+\dfrac{\pi}{6}\right)=-1\Leftrightarrow x+\dfrac{\pi}{6}=-\dfrac{\pi}{2}+k2\pi\Leftrightarrow x=-\dfrac{2}{3}\pi+k2\pi\)

1: \(y=\sqrt{3}\cdot sin^2x-\left(1-sin^2x\right)+5\)
\(=sin^2x\left(\sqrt{3}+1\right)-1+5=sin^2x\left(\sqrt{3}+1\right)+4\)
\(0< =sin^2x< =1\)
=>\(0< =sin^2x\left(\sqrt{3}+1\right)< =\sqrt{3}+1\)
=>4<=y<=căn 3+5
y min=4 khi sin^2x=0
=>sin x=0
=>x=kpi
\(y_{max}=5+\sqrt{3}\) khi \(sin^2x=1\)
=>\(cos^2x=0\)
=>cosx=0
=>\(x=\dfrac{pi}{2}+kpi\)
2: \(y=5\left[\dfrac{3}{5}sinx+\dfrac{4}{5}cosx\right]+7\)
\(=5\cdot\left[sinx\cdot cosa+cosx\cdot sina\right]+7\)(Với cosa=3/5; sin a=4/5)
\(=5\cdot sin\left(x+a\right)+7\)
-1<=sin(x+a)<=1
=>-5<=5sin(x+a)<=5
=>-5+7<=y<=5+7
=>2<=y<=12
\(y_{min}=2\) khi sin (x+a)=-1
=>x+a=-pi/2+kp2i
=>\(x=-\dfrac{pi}{2}+k2pi-a\)
\(y_{max}=12\) khi sin(x+a)=1
=>x+a=pi/2+k2pi
=>\(x=\dfrac{pi}{2}+k2pi-a\)

ĐKXĐ; ...
\(\Leftrightarrow\frac{3}{5}sinx+\frac{4}{5}cosx-1=\frac{1}{5}\left(4tanx-3\right)^2\)
\(\Leftrightarrow sin\left(x+a\right)-1=\frac{1}{5}\left(4tanx-3\right)^2\)
(Trong đó \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{3}{5}\))
Do \(\left\{{}\begin{matrix}sin\left(x+a\right)-1\le0\\\left(4tanx-3\right)^2\ge0\end{matrix}\right.\) \(\forall a;x\) nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sin\left(x+a\right)=1\\4tanx-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3sinx+4cosx=5\\4sinx-3cosx=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sinx=\frac{3}{5}\\cosx=\frac{4}{5}\end{matrix}\right.\) \(\Rightarrow x=arcsin\left(\frac{3}{5}\right)+k2\pi\)

Đặt \(t=3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)\)
\(\Rightarrow-5\le t\le5\)
\(\Rightarrow y=t^2-t+m\)
\(y>0\) ; \(\forall m\Leftrightarrow t^2-t+m>0\Leftrightarrow m>-t^2+t\) ; \(\forall m\)
\(\Leftrightarrow m>\max\limits_{\left[-5;5\right]}\left(-t^2+t\right)\)
Mà \(-t^2+t=-\left(t-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
\(\Rightarrow m>\frac{1}{4}\)

a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)
b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)
Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)
\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)
Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)
Pttt:\(cos3x.cosa+sin3a.sina=1\)
\(\Leftrightarrow cos\left(3x-a\right)=1\)
\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))
Vậy...
1)\(1+2sinx=2cosx\)
\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)
\(\Leftrightarrow sin2x=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)
b) \(4cosx-3sinx=3\)
\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)
Khi đó:
\(sinacosx-cosasinx=\dfrac{3}{5}\)
\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
3)\(3cos3x+4sin3x=5\)
\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)
Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)
khi đó: \(sinacos3x+cosasin3x=1\)
\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)
Chúc bạn học tốt^^

Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)

chi 2 vế cho -5
<=>−35sinx+45cosx=1−35sinx+45cosx=1
đặt 35=sina35=sina
=>cosa=4545
=>cos(x+a)=1