Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đkxđ: \(x\ne1,x\ne0\)
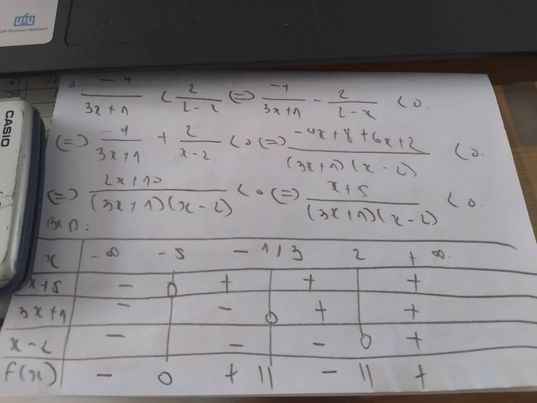
⇔x+1x−1+2>x−1x⇔2x−1+2>−1x⇔x+1x−1+2>x−1x⇔2x−1+2>−1x
⇔2x−1+1x+2>0⇔2x+x−1+2(x2−x)(x−1)x=2x2+x−1(x−1)(x)>0⇔2x−1+1x+2>0⇔2x+x−1+2(x2−x)(x−1)x=2x2+x−1(x−1)(x)>0
Tử {delta =9}
−1<x<12⇒Tử<0
0<x<1⇒M<0
Nghiệm BPT là
[x<−10<x<12 hoặc x>1

a)
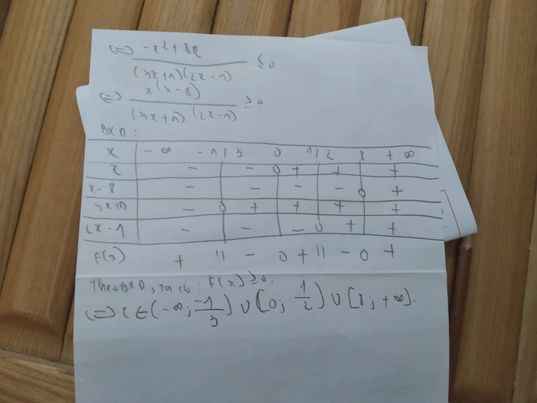
x^2 +1 >0 mọi x
BPT \(\Leftrightarrow x^2+3x-10< 0\) {\(\Delta=9+40=49\)}
\(\Rightarrow-5< x< 2\)
b)
5+x^2 > 0 với mọi x BPT \(\Leftrightarrow20-2x-x^2-5>0\Leftrightarrow x^2+2x-15< 0\){\(\Delta'=1+15=16\)}
\(\Rightarrow-5< x< 3\)

lời giải
a) \(\left\{{}\begin{matrix}-2x+\dfrac{3}{5}>\dfrac{2x-7}{3}\left(1\right)\\x-\dfrac{1}{2}< \dfrac{5\left(3x-1\right)}{2}\left(2\right)\end{matrix}\right.\)
(1)\(\Leftrightarrow\)
\(\dfrac{3}{5}+\dfrac{7}{3}>\left(\dfrac{2}{3}+2\right)x\)
\(\dfrac{44}{15}>\dfrac{8}{3}x\) \(\Rightarrow x< \dfrac{44.3}{15.8}=\dfrac{11}{5.2}=\dfrac{11}{10}\)
Nghiêm BPT(1) là \(x< \dfrac{11}{10}\)
(2) \(\Leftrightarrow2x-1< 15x-5\Rightarrow13x>4\Rightarrow x>\dfrac{4}{13}\)
Ta có: \(\dfrac{4}{13}< \dfrac{11}{10}\) => Nghiệm hệ (a) là \(\dfrac{4}{13}< x< \dfrac{11}{10}\)

a)
<=> f(x) = .
Xét dấu của f(x) ta được tập nghiệm của bất phương trình:
T = ∪ [3; +∞).
b)
<=> f(x) = =
.
f(x) không xác định với x = ± 1.
Xét dấu của f(x) cho tập nghiệm của bất phương trình:
T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3).
c) <=> f(x) =
= .
Tập nghiệm: \(\left(-12;-4\right)\cup\left(-3;0\right)\).

a) Tương đương. vì nhân hai vế bất phương trình thứ nhất với -1 và đổi chiều bất phương trình thì được bất phương trình thứ 2.
b) Chuyển vế các hạng tử vế phải và đổi dấu ở bất phương trình thứ nhất thì được bất phương trình thứ tương đương.
c) Tương đương. Vì cộng hai vế bất phương trình thứ nhất với với mọi x ta được bất phương trình thứ 3.
d) Điều kiện xác định bất phương trình thứ nhất: D ={x ≥ 1}.
2x + 1 > 0 ∀x ∈ D. Nhân hai vế bất phương trình thứ hai. Vậy bất phương trình tương đương.

a) \(4x^2-x+1< 0\)
Tam thức f(x) = 4x2 - x + 1 có hệ số a = 4 > 0 biệt thức ∆ = 12 – 4.4 < 0. Do đó f(x) > 0 ∀x ∈ R.
Bất phương trình 4x2 - x + 1 < 0 vô nghiệm.
b) f(x) = - 3x2 + x + 4 = 0
\(\Delta=1^2-4\left(-3\right).4=49\)
\(x_1=\dfrac{-1+\sqrt{49}}{-3}=-1\)
\(x_2=\dfrac{-1-\sqrt{49}}{-3.2}=\dfrac{4}{3}\)
- 3x2 + x + 4 ≥ 0 <=> - 1 ≤ x ≤ .

\(\Leftrightarrow\dfrac{1}{x-1}>\dfrac{1}{x-2}-\dfrac{1}{x+2}=\dfrac{\left(x+2\right)-\left(x-2\right)}{x^2-4}=\dfrac{4}{x^2-4}\)\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{4}{x^2-4}>0\Leftrightarrow\dfrac{x^2-4-4x+4}{\left(x-2\right)\left(x-1\right)\left(x+2\right)}>0\)
\(\Leftrightarrow A=\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x-1\right)\left(x+2\right)}>0\)
Điều kiện tồn tại A
\(\left\{{}\begin{matrix}x\ne2\\x\ne1\\x\ne-2\end{matrix}\right.\) \(\Rightarrow A=\dfrac{x}{\left(x-1\right)\left(x+2\right)}\)
\(\left\{{}\begin{matrix}x>0\\\left[{}\begin{matrix}x< -2\\x>1\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow x>1\)(1)
\(\left\{{}\begin{matrix}x< 0\\-2< x< 1\end{matrix}\right.\) \(\Rightarrow-2< x< 0\)(2)
từ (1)&(2)kết luận\(\Rightarrow\left[{}\begin{matrix}-2< x< 0\\x>1\end{matrix}\right.\)