Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{x-5}{4}\ge\dfrac{3-2x}{5}\)
\(\Leftrightarrow\dfrac{5x-25}{20}\ge\dfrac{12-8x}{20}\)
\(\Leftrightarrow5x-25\ge12-8x\)
\(\Leftrightarrow5x+8x\ge12+25\)
\(\Leftrightarrow13x\ge37\)
\(\Leftrightarrow x\ge\dfrac{37}{13}\)
b)\(2x\left(6x-1\right)-3< 3x\left(4x+3\right)-5x\)
\(\Leftrightarrow12x^2-2x-3< 12x^2+9x-5x\)
\(\Leftrightarrow12x^2-12x^2-2x-9x+5x< 3\)
\(\Leftrightarrow-6x< 3\)
\(\Leftrightarrow x>-\dfrac{1}{2}\)
c)\(\left|x-4\right|=5-3x\)
\(\Leftrightarrow\left[{}\begin{matrix}5-3x=x-4\\5-3x=4-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5+4=x+3x\\5-4=-x+3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=9\\2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{4}\\x=\dfrac{1}{2}\end{matrix}\right.\)
p/s: tui làm đúng đề
a.
\(\dfrac{x-5}{4}\ge\dfrac{3-2x}{5}\)
\(\Leftrightarrow5x-25\ge12-8x\)
\(\Leftrightarrow13x\ge37\)
\(\Leftrightarrow x\ge\dfrac{37}{13}\)
0 37 13
b.
\(2x\left(6x-1\right)-3< 3x\left(4x+3\right)-5x\)
\(\Leftrightarrow12x^2-2x-3< 12x^2+9x-5x\)
\(\Leftrightarrow-6x>3\)
\(\Leftrightarrow x< \dfrac{-1}{2}\)
0 -1 2

\(a,2x-6< 0\Leftrightarrow2x>6\Leftrightarrow x>3\)
\(b,5x+2x< 4+25\Leftrightarrow7x< 29\Leftrightarrow x< \frac{29}{7}\)
\(c,-5x+6>8-10+8x\Leftrightarrow-5x-8x>8-10-6\)
\(-13x>-8\Leftrightarrow x< \frac{8}{13}\)
\(d,3x-12\le2-4x\Leftrightarrow3x+4x\le2+12\)
\(\Leftrightarrow7x\le14\Leftrightarrow x\le2\)
\(e,\frac{3\left(x-3\right)}{6}>\frac{2\left(2x-5\right)}{6}+\frac{6}{6}\Rightarrow3x-9>4x-10+6\)
\(\Leftrightarrow3x-4x>-4+9\Leftrightarrow x>-5\)
\(f,3\left(2x-3\right)>1+2\left(2+2x\right)\Leftrightarrow6x-9>1+4+4x\)
\(6x-4x>14\Leftrightarrow2x>14\Leftrightarrow x>7\)
Tự biểu diễn nha!

\(\dfrac{2x-3}{2}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow\dfrac{3\left(2x-3\right)}{6}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow3\left(2x-3\right)>8x-11\)
\(\Leftrightarrow6x-9>8x-11\)
\(\Leftrightarrow-2x>-2\)
\(\Leftrightarrow x< 1\)
Vậy \(S=\left\{x|x< 1\right\}\)
\(2x-3\le8x-11\)
\(\Leftrightarrow-6x\le-8\)
\(\Leftrightarrow x\ge\dfrac{8}{6}\)
Vậy \(S=\left\{x|x\ge\dfrac{8}{6}\right\}\)

a) 2x - 3 > 3(x - 2)
<=> 2x - 3 > 3x - 6
<=> -x > -3
<=> x < 3
b) \(\frac{12x+1}{12}\le\frac{9x+1}{3}-\frac{8x+1}{4}\)
\(\Leftrightarrow\frac{12x+1}{12}\le\frac{4\left(9x+1\right)}{12}-\frac{3\left(8x+1\right)}{12}\)
\(\Leftrightarrow12x+1\le36x+4-24x-3\)
\(\Leftrightarrow0x\le0\)
=> bpt vô số nghiệm
(Bạn tự biểu diễn tập nghiệm nha)
a) Thay x = 3 vào bất phương trình ta được: 2.3 + 3 < 9 <=> 9 < 9 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình2x + 3 < 9
b) Thay x = 3 vào bất phương trình ta có: -4.3 > 2.3 + 5 => -12 > 11 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình -4x > 2x + 5
c) Thay x = 3 vào bất phương trình ta có: 5 - 3 > 3.3 -12 => 2 > -3 (khẳng định đúng)
Vậy x = 3 là nghiệm của bất phương trình 5 - x > 3x - 12

a:=>3x=15
=>x=5
b: =>8-11x<52
=>-11x<44
=>x>-4
c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)
\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)

Câu 1a : tự kết luận nhé
\(2\left(x+3\right)=5x-4\Leftrightarrow2x+6=5x-4\Leftrightarrow-3x=-10\Leftrightarrow x=\frac{10}{3}\)
Câu 1b : \(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)ĐK : \(x\ne\pm3\)
\(\Leftrightarrow x+3-2x+6=5-2x\Leftrightarrow-x+9=5-2x\Leftrightarrow x=-4\)
c, \(\frac{x+1}{2}\ge\frac{2x-2}{3}\Leftrightarrow\frac{x+1}{2}-\frac{2x-2}{3}\ge0\)
\(\Leftrightarrow\frac{3x+3-4x+8}{6}\ge0\Rightarrow-x+11\ge0\Leftrightarrow x\le11\)vì 6 >= 0
1) 2(x + 3) = 5x - 4
<=> 2x + 6 = 5x - 4
<=> 3x = 10
<=> x = 10/3
Vậy x = 10/3 là nghiệm phương trình
b) ĐKXĐ : \(x\ne\pm3\)
\(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)
=> \(\frac{x+3-2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{5-2x}{\left(x-3\right)\left(x+3\right)}\)
=> x + 3 - 2(x - 3) = 5 - 2x
<=> -x + 9 = 5 - 2x
<=> x = -4 (tm)
Vậy x = -4 là nghiệm phương trình
c) \(\frac{x+1}{2}\ge\frac{2x-2}{3}\)
<=> \(6.\frac{x+1}{2}\ge6.\frac{2x-2}{3}\)
<=> 3(x + 1) \(\ge\)2(2x - 2)
<=> 3x + 3 \(\ge\)4x - 4
<=> 7 \(\ge\)x
<=> x \(\le7\)
Vậy x \(\le\)7 là nghiệm của bất phương trình
Biểu diễn
-----------------------|-----------]|-/-/-/-/-/-/>
0 7
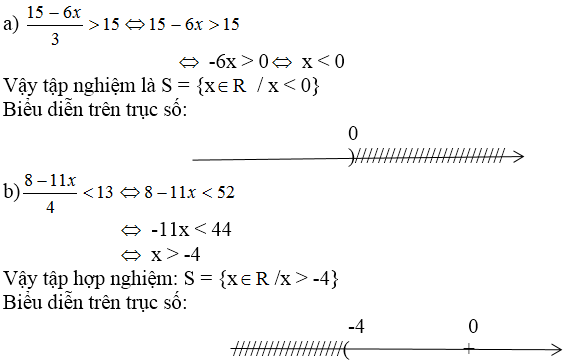
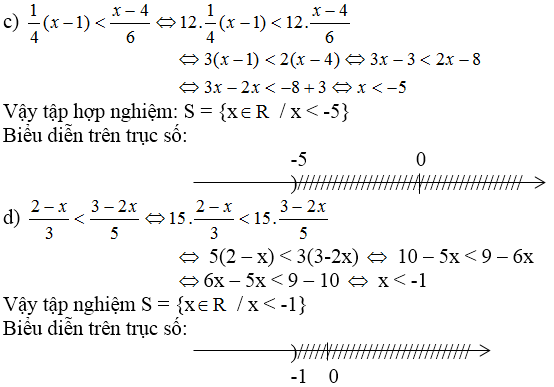
a/ \(\dfrac{2-x}{3}< \dfrac{3-2x}{5}\)
\(\Leftrightarrow5\left(2-x\right)< 3\left(3-2x\right)\)
\(\Leftrightarrow10-5x< 9-6x\)
\(\Leftrightarrow x< -1\)
Bpt có tập nghiệm: \(S=\left\{x|x>-1\right\}\)
Biểu diễn tập nghiệm trên trục số:
-1 0
b/ 8x + 3(x+1) > 5x - (2x - 6)
<=> 8x + 3x + 3 > 5x - 2x + 6
<=> 8x + 3x - 5x + 2x > 6 - 3
<=> 8x > 3 <=> x > \(\dfrac{8}{3}\)
Vậy bpt có tập nghiệm là: \(S=\left\{x|x>\dfrac{8}{3}\right\}\)
Biểu diễn........(tự biểu diễn nhé quá dễ r)
c/ \(\left|x-7\right|=-2x+3\) (*)
+) Nếu \(x-7\ge0\Leftrightarrow x\ge7\) thì
|x - 7| = x - 7
(*) => x - 7 = -2x + 3
<=> x + 2x = 3 + 7
<=> 3x = 10 <=> x = \(\dfrac{10}{3}\)(loại)
+) Nếu x - 7 < 0 <=> x < 7
thì |x - 7| = 2x - 3
(*) => x - 7 = 2x - 3
<=> x - 2x = -3 + 7
<=> -x = 4 <=> x = -4 (nhận)
Vậy pt có 1 nghiệm x = -4
a.
\(\dfrac{2-x}{3}< \dfrac{3-2x}{5}\)
\(\Leftrightarrow10-5x< 9-6x\)
\(\Leftrightarrow x< -1\)
\(\Leftrightarrow x< -1\)