
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

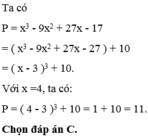

x=11 suy ra 12=x+1 thay vào A ta có:
A=x^17- (x+1)x^16 + (x+1)x^15 - (x+1)x^14 + .....- (x+1)x^2+(x+1)x -1
= x^17 - x^17 -x^16 + x^16 + x^15 - x^15 - x^14 +.....- x^3 -x^2 + x^2 +x -1
= x-1= 11-1=10

+) \(A=x^2+2x-9=x^2+2x+1-10=\left(x+1\right)^2-10\ge-10\)
Min A = -10 \(\Leftrightarrow x=-1\)
+) \(B=x^2+5x-1=x^2+5x+\frac{25}{4}-\frac{29}{4}=\left(x+\frac{5}{2}\right)^2-\frac{29}{4}\ge\frac{-29}{4}\)
Min B = -29/4 \(\Leftrightarrow x=\frac{-5}{2}\)
+) \(C=x^2+4x=x^2+4x+4-4=\left(x+2\right)^2-4\ge-4\)
Min C = -4 \(\Leftrightarrow x=-2\)
+) \(D=x^2-8x+17=x^2-8x+16+1=\left(x-4\right)^2+1\ge1\)
Min D = 1 \(\Leftrightarrow x=4\)
+) \(E=x^2-7x+1=x^2-7x+\frac{49}{4}-\frac{45}{4}=\left(x-\frac{7}{2}\right)-\frac{45}{4}\ge-\frac{45}{4}\)
Min E = -45/4 \(\Leftrightarrow x=\frac{7}{2}\)
A = x2 + 2x - 9
= ( x2 + 2x + 1 ) - 10
= ( x + 1 )2 - 10 ≥ -10 ∀ x
Đẳng thức xảy ra <=> x + 1 = 0 => x = -1
=> MinA = -10 <=> x = -1
B = x2 + 5x - 1
= ( x2 + 5x + 25/4 ) - 29/4
= ( x + 5/2 )2 - 29/4 ≥ -29/4 ∀ x
Đẳng thức xảy ra <=> x + 5/2 = 0 => x = -5/2
=> MinB = -29/4 <=> x = -5/2
C = x2 + 4x
= ( x2 + 4x + 4 ) - 4
= ( x + 2 )2 - 4 ≥ -4 ∀ x
Đẳng thức xảy ra <=> x + 2 = 0 => x = -2
=> MinC = -4 <=> x = -2
D = x2 - 8x + 17
= ( x2 - 8x + 16 ) + 1
= ( x - 4 )2 + 1 ≥ 1 ∀ x
Đẳng thức xảy ra <=> x - 4 = 0 => x = 4
=> MinD = 1 <=> x = 4
E = x2 - 7x + 1
= ( x2 - 7x + 49/4 ) - 45/4
= ( x - 7/2 )2 - 45/4 ≥ -45/4 ∀ x
Đẳng thức xảy ra <=> x - 7/2 = 0 => x = 7/2
=> MinE = -45/4 <=> x = 7/2

a, ĐKXĐ: \(x\ne-3\) và \(x\ne\pm1\)
b, \(P=\frac{x\left(x+3\right)-11+x^2-3x+9}{x^3+27}:\frac{x^2-1}{x+3}\)
\(P=\frac{2x^2-2}{x^3+27}.\frac{x+3}{x^2-1}\)
\(=\frac{2\left(x-1\right)\left(x+1\right)}{\left(x+3\right)\left(x^2-3x+9\right)}.\frac{x+3}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{2}{x^2-3x+9}\)
c, \(P=\frac{2}{x^2-3x+9}==\frac{2}{\left(x-\frac{3}{2}\right)^2+\frac{27}{4}}\le\frac{2}{\frac{27}{4}}=\frac{8}{27}\)
Dấu "=" xảy ra khi: \(x-\frac{3}{2}=0\Leftrightarrow x=\frac{3}{2}\)
Vậy P lớn nhất bằng \(\frac{8}{27}\) \(\Leftrightarrow x=\frac{3}{2}\)
\(P=\left(\frac{x}{x^2-3x+9}-\frac{11}{x^3+27}+\frac{1}{x+3}\right):\frac{x^2-1}{x+3}.\)
ĐKXĐ : \(x\ne-3;x\ne0\)
\(P=\left(\frac{x\left(x+3\right)}{\left(x+3\right)\left(x^2-3x+9\right)}-\frac{11}{\left(x+3\right)\left(x^2-3x+9\right)}+\frac{x^2-3x+9}{\left(x+3\right)\left(x^2-3x+9\right)}\right).\frac{x+3}{x^2-1}\)
\(P=\left(\frac{x^2+3x-11+x^2-3x+9}{\left(x+3\right)\left(x^2-3x+9\right)}\right).\frac{x+3}{x^2-1}\)
\(P=\frac{2x^2-2}{\left(x^2-3x+9\right)}.\frac{1}{x^2-1}=\frac{2\left(x^2-1\right)}{\left(x^2-3x+9\right)}.\frac{1}{x^2-1}\)
\(P=\frac{2}{x^2-3x+9}\)

a) Để \(\frac{17}{3-x}\) đạt giá trị nguyên lớn nhất
=> 3 - x đạt giá trị nhỏ nhất \(\left(3-x\ne0\right)\) ( x thuộc Z)
\(3-x\ge1\)
Dấu "=" xảy ra khi
3-x = 1
x = 2
=> giá trị lớn nhất của 17/3-x = 17/3-2 = 17/1 = 17
KL: giá trị lớn nhất của 17/3-x là 17 tại x = 2
b) Đặt \(B=\frac{32-2x}{11-x}=\frac{12+22-2x}{11-x}=\frac{12+2.\left(11-x\right)}{11-x}=\frac{12}{11-x}+2\)
Để B đạt giá trị nguyên lớn nhất
=> 12/11-x đạt giá trị nguyên lớn nhất
=> 11 - x đạt giá trị nguyên nhỏ nhất ( 11 - x khác 0, x thuộc Z)
\(11-x\ge1\)
Dấu "=" xảy ra khi
11 - x = 1
x = 10
=> giá trị lớn nhất của B là: B = 12/11-x +2 = 12/11-10 + 2 = 12/1 + 2 = 12 + 2 = 14
KL: giá trị lớn nhất của B = 14 tại x = 10

x=11
nên x+1=12
\(x^4-12x^3+12x^2-12x+111\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+111\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+111\)
=111-x
=111-11=100

C = -( 9x2 -2x +1) -17
= -(3x-1)2-17
ta có -(3x-1)2 bé hơn hoặc bằng 0 với mọi x
nên -(3x-1)2 -17 bé hơn hoặc bằng -17 với mọi x
vậy.............
\(C=-9x^2+2x-17\)
\(=-9\left(x^2-2.\dfrac{1}{9}x+\dfrac{1}{81}\right)-\dfrac{152}{9}\)
\(=-9\left(x-\dfrac{1}{9}\right)^2-\dfrac{152}{9}\)
Vì \(-9\left(x-\dfrac{1}{9}\right)^2\le0\)
Nên \(-9\left(x-\dfrac{1}{9}\right)^2-\dfrac{152}{2}\le0\)
Vậy C luôn âm với mọi giá trị của biến
\(D=-5x^2-6x-11\)
\(=-5\left(x^2+2.\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{46}{5}\)
\(=-5\left(x+\dfrac{3}{5}\right)^2-\dfrac{46}{5}\)
Vì \(-5\left(x+\dfrac{3}{5}\right)^2\le0\)
Nên \(-5\left(x+\dfrac{3}{5}\right)^2-\dfrac{46}{5}\le0\)
vậy D luôn âm với mọi giá trị của biến
\(E=\dfrac{-1}{4}x^2+3x-15\)
\(=-\dfrac{1}{4}\left(x^2-12x+36\right)-6\)
\(=-\dfrac{1}{4}\left(x-6\right)^2-6\le0\)
Vậy E luôn âm với mọi giá trị

\(B=x^5-15x^4+16x^3-29x^2+13x\)
\(=x^5-14x^4-x^4+14x^3+2x^3-28x^2-x^2+14x-x+14-14\)
\(=x^4\left(x-14\right)-x^3\left(x-14\right)+2x^2\left(x-14\right)-x\left(x-14\right)-\left(x-14\right)-14\)
\(=\left(x^4-x^3+2x^2-x-1\right)\left(x-14\right)-14\)
Thay x = 14 => B = -14
Vậy...
phần còn lại tách ra làm tương tự nhé