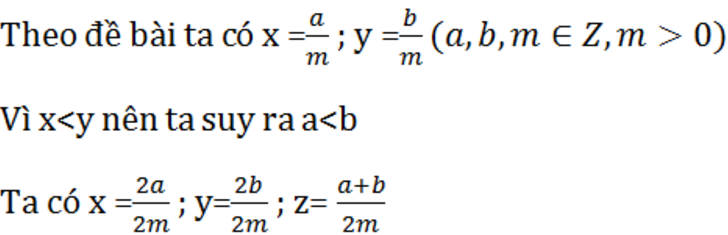Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo câu hỏi : Câu hỏi của Thiên Thiên - Toán lớp 7 | Học trực tuyến

Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b nên a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) => x < z < y (đpcm)

Theo đề bài ta có x = \(\frac{a}{m}\) , y = \(\frac{b}{m}\)( a, b, m \(\in\) Z, m > 0 )
Vì x < y nên ta suy ra a < b
Ta có : x = \(\frac{2a}{2m}\), y = \(\frac{2b}{2m}\), , z = \(\frac{a+b}{2m}\)
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y

Ta có x < y
=> x + x < y + x
=> \(\frac{2a}{m}<\frac{a+b}{m}\)
=> 2a < a + b
=> x + y < y + y
=> \(\frac{a+b}{m}<\frac{2b}{m}\)
=> a + b < 2b
Mà x = \(\frac{a}{m}\)=\(\frac{2a}{2m}\)
y = \(\frac{b}{m}\)=\(\frac{2b}{2m}\)
Theo giả thuyết trên
=> 2a < a + b < 2b
=> \(\frac{2a}{2m}<\frac{a+b}{2m}<\frac{2b}{2m}\)
=> x < z < y (Đpcm)

Hoàng Anh Thư mk nghĩ x = \(\frac{a}{m}\) , như tkế mk làm đc , còn như x = \(\frac{a}{b}\) tkì mk chịu thôi !!
![]()

Ta có : x < y mà \(x=\frac{a}{m}\)và \(y=\frac{b}{m}\)
\(\Rightarrow a< b\)
a<b \(\Rightarrow a+a< b+a\)
\(\text{Hay}\)\(2a< b+a\)
\(\Rightarrow\frac{a+b}{2m}>\frac{2a}{2m}\)
\(\Rightarrow z>x\)( 1)
a < b \(\Rightarrow a+b< b+b\)
Hay \(a+b< 2b\)
\(\Rightarrow\frac{a+b}{2m}< \frac{2b}{2m}\)
\(\Rightarrow z< y\)(2)
Từ (1) và (2) suy ra : x < z < y (đpcm)
\(x< y\Rightarrow\frac{a}{m}< \frac{b}{m}\Rightarrow a< b\)
\(\Rightarrow\frac{a}{2m}+\frac{a}{2m}< \frac{a}{2m}+\frac{b}{2m}< \frac{b}{2m}+\frac{b}{2m}\)
\(\Rightarrow\frac{2a}{2m}< \frac{a+b}{2m}< \frac{2b}{2m}\)
\(\Rightarrow\frac{a}{m}< \frac{a+b}{2m}< \frac{b}{m}\)
\(\Rightarrow x< z< y\)