
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: a = -1/8 = -9/72
b = 2/-9 = -2/9 = -16/72
Ta thấy: -9 > -16 => -9/72 > -16/72
hay a > b
Vậy a > b
b) Ta có: a = 12/15 = 4/5= 16/20
b = -( -3/4 ) = 3/4= 15/20
Ta thấy: 16 > 15 => 16/20 > 15/20
hay a > b
Vậy a > b
c) Ta có: a = -2/3 = -40/60
b = -0,65 = -13/20 = -39/60
Ta thấy: -40 < -39 => -40/60 < -39/60
hay a < b
Vậy a < b
d) Ta có: a = -21/3 = -7
b = -413% = -4,13
Ta thấy: -7 < -4,13
=> a < b
Vậy a < b
Chuk bn hok tốt! ![]()
![]()

Vì \(\left|x-3,5\right|\ge0\); \(\left|4,5-x\right|\ge0\)
=> \(\left|x-3,5\right|+\left|4,5-x\right|\ge0\)
Mà theo đề bài: \(\left|x-3,5\right|+\left|4,5-x\right|=0\)
=> \(\begin{cases}\left|x-3,5\right|=0\\\left|4,5-x\right|=0\end{cases}\)=> \(\begin{cases}x-3,5=0\\4,5-x=0\end{cases}\)=> \(\begin{cases}x=3,5\\x=4,5\end{cases}\), vô lý vì x không thể cùng đồng thời nhận 2 giá trị khác nhau
Vậy không tồn tại giá trị của x thỏa mãn đề bài

\(A=3^0+3^1+3^2+...+3^{2018}\)
\(3A=3^1+3^2+3^3+...+3^{2018}+3^{2019}\)
\(\Rightarrow3A-A=\left(3^1+3^2+...+3^{2019}\right)-\left(3^0+3^1+...+3^{2018}\right)\)
\(2A=3^{2019}-3^0=3^{2019}-1\)
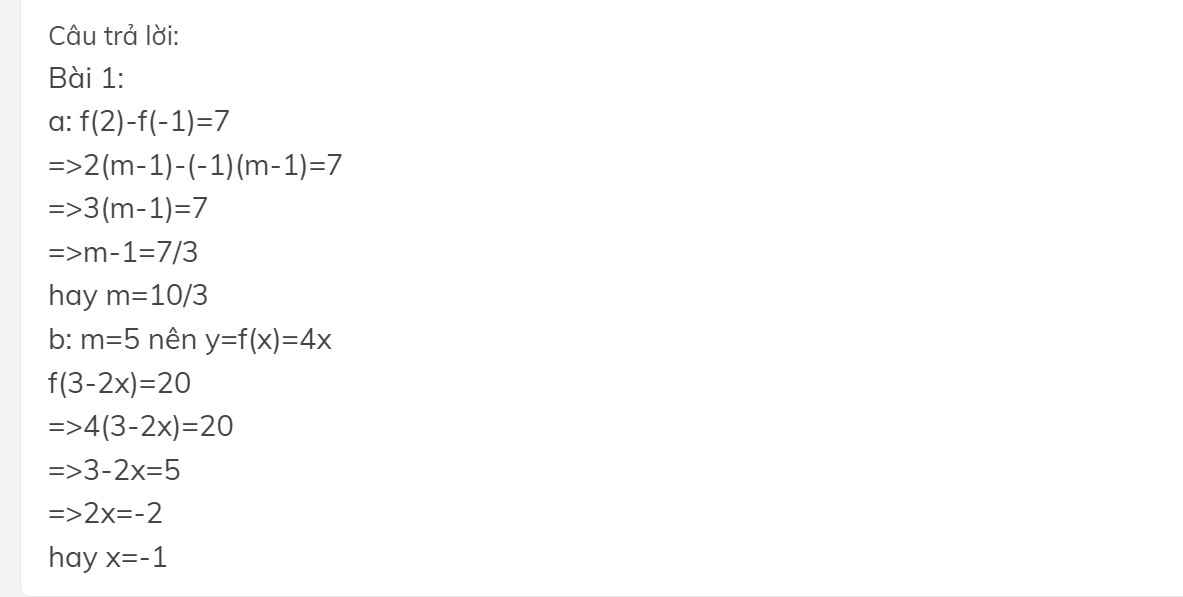
 Anhr mik tìm đc nha bn !!!
Anhr mik tìm đc nha bn !!!
\(-2x^2-8x=0\)
\(\Leftrightarrow-2x\left(x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x=0\\x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-4\end{cases}}}\)
#H