
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: P(x)=5x^2-4x+7
Sửa đề: Q(x)=-5x^3-x^2+4x-5
Q(x)+P(x)+5x^2-2=0
=>5x^2-4x+7-5x^3-x^2+4x-5+5x^2-2=0
=>5x^3=0
=>x=0
ÉT Ô ÉT
Câu 3: Tìm x biết:
|x + 1| + |x + 2| + |x + 2020| = 4x
Giúp mik với!!!
Mik hứa Tick cho… Pls

TH1 : \(x< -2020\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) - ( x + 2020 ) = 4x
<=> -3x - 2023 = 4x <=> -7x = 2023 <=> x = -289
TH2 : \(-2020\le x< -2\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) + x + 2020 = 4x
<=> -x + 2017 = 4x
<=> -5x = -2017 <=> x = 2017/5 ( = 403,4 )
TH3 : \(-2\le x< -1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) + x + 2 + x + 2020 = 4x
<=> x + 2021 = 4x <=> -3x = -2021 <=> x = 2021/3
TH4 : \(x>-1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = x + 1 + x + 2 + x + 2020 = 4x
<=> 3x + 2023 = 4x
<=> -x = -2023 <=> x = 2023
Vậy...
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.

a: A(x)=x^5+3x^4-2x^3-9x^2+11x-6
B(x)=x^5+3x^4-2x^3-10x^2+9x-8
C(x)=A(x)-B(x)
=x^5+3x^4-2x^3-9x^2+11x-6-x^5-3x^4+2x^3+10x^2-9x+8
=x^2+2x+2
b; C(x)=2x+2
=>x^2=0
=>x=0
c: C(x)=2012
=>x^2+2x-2010=0
Δ=2^2-4*1*(-2010)=8044>0
=>Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{8044}}{2}\simeq-45,84\left(loại\right)\\x_2=\dfrac{-2+\sqrt{8044}}{2}\simeq43,84\left(loại\right)\end{matrix}\right.\)
=>Ko có giá trị nguyên của x thỏa mãn

\(a,A=x^3+3x^2-4x-12\)
\(=x^2\left(x+3\right)-4\left(x+3\right)\)
\(=\left(x^2-4\right)\left(x+3\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x+3\right)\)
Thay \(x=2\) vào A, ta được:
\(A=\left(2-2\right)\left(2+2\right)\left(2+3\right)\)
\(=0\)
⇒ \(x=2\) là nghiệm của A
\(B=-2x^3+3x^2+4x+1\)
Thay \(x=2\) vào B, ta được:
\(B=-2\cdot2^3+3\cdot2^2+4\cdot2+1\)
\(=-16+12+8+1\)
\(=5\)
⇒ \(x=2\) không là nghiệm của B
\(b,A+B=x^3+3x^2-4x-12+\left(-2x^3\right)+3x^2+4x+1\)
\(=\left[x^3+\left(-2x^3\right)\right]+\left(3x^2+3x^2\right)+\left(-4x+4x\right)+\left(-12+1\right)\)
\(=-x^3+6x^2-11\)
\(A-B=x^3+3x^2-4x-12-\left(-2x^3+3x^2+4x+1\right)\)
\(=x^3+3x^2-4x-12+2x^3-3x^2-4x-1\)
\(=\left(x^3 +2x^3\right)+\left(3x^2-3x^2\right)+\left(-4x-4x\right)+\left(-12-1\right)\)
\(=3x^3-8x-13\)
#\(Toru \)

a: AC=căn 4,5^2+6^2=7,5cm
b: Xét ΔFBC có
H là trung điểm của CB
HA//FB
=>A là trung điểm của FC
ΔFBC vuông tại B có BA là trung tuyến
nên BA=AF
=>ΔAFB cân tại A

3xy + y=4-x
<=>9xy+3y=12-3x
<=>9xy+3y+3x+1=13
<=>3y.(3x+1)+(3x+1)=13
<=>(3x+1)(3y+1)=13
<=> *{3x+1=13y+1=13{3x+1=13y+1=13<=>{x=0y=4{x=0y=4(nhận)
*{3x+1=123y+1=1{3x+1=123y+1=1<=>{x=4y=0{x=4y=0(nhận)
*{3x+1=−13y+1=−13{3x+1=−13y+1=−13<=>{x=−23y=−143{x=−23y=−143(loại)
*{3x+1=−133y+1=−1{3x+1=−133y+1=−1<=>{x=−143y=−23{x=−143y=−23(loại)
Vậy x=4 thì y=0 ; x=0 thì y=4

\(\left(1-x\right)^2=2003.\left(x-1\right)\)
\(\left(1-x\right)^2-2003\left(x-1\right)=0\)
\(\left(1-x\right)^2+2003\left(1-x\right)=0\)
\(\left(1-x\right)\left(1-x+2003\right)=0\)
\(\left(1-x\right)\left(2004-x\right)=0\)
\(TH1:1-x=0\)
\(x=1\)
\(TH2:2004-x=0\)
\(x=2004\)
vậy........

\(C=\dfrac{-1}{5}+\left(\dfrac{1}{-5}\right)^2+\left(-\dfrac{1}{5}\right)^3+...+\left(-\dfrac{1}{5}\right)^{99}\)
=>\(5\cdot C=-1+\left(-\dfrac{1}{5}\right)+\left(-\dfrac{1}{5}\right)^2+...+\left(-\dfrac{1}{5}\right)^{98}\)
=>\(5\cdot C-C=\left(-1\right)-\left(-\dfrac{1}{5}\right)^{99}\)
=>\(4C=-1+\dfrac{1}{5^{99}}=\dfrac{-5^{99}+1}{5^{99}}\)
=>\(C=\dfrac{-5^{99}+1}{4\cdot5^{99}}\)
(x-3y)^2006+(y+4)^2008=0
=>x-3y=0 và y+4=0
=>x=3y và y=-4
=>x=3*(-4)=-12 và y=-4
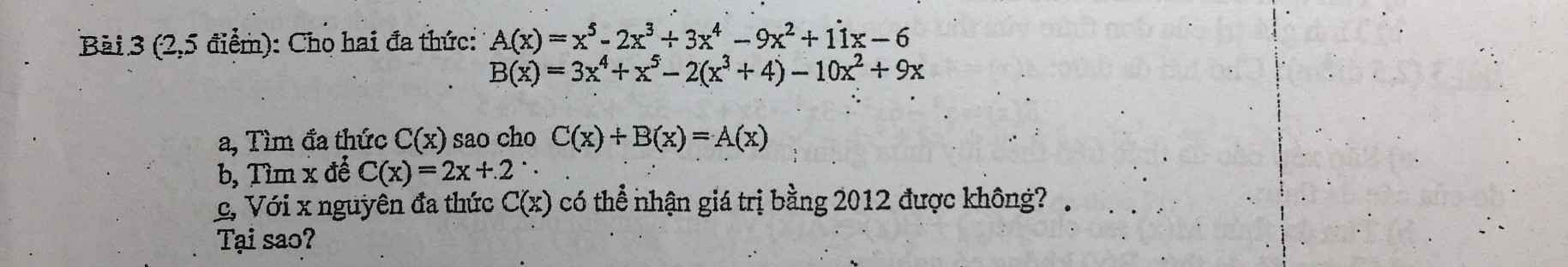 GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
|th|i |th|ì |th|ôi
nà ní