Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

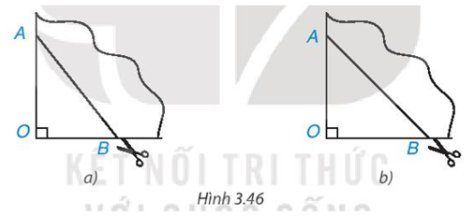
- Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
- Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

Tứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

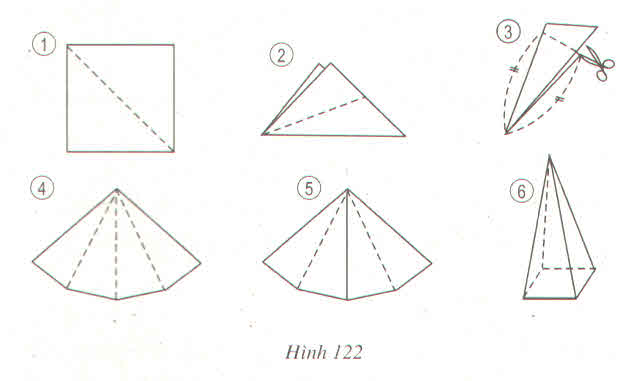
Vì gấp làm 1 phần tư và cắt 1 nhát kéo thành 1 tam giác nên khi mở ra sẽ là 4 tam giác bằng nhau
=> tứ giác đó có 4 cạnh là 4 cạnh huyền của 4 tam giác bằng nhau nên tứ giác đó có 4 cạnh bằng nhau
=> tứ giác đó là hình thoi

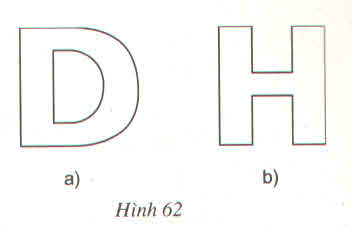
a) Cắt được chứ D với nét gấp là trục đối xứng ngang của chữ D,
Các chứ cái có trục đối xứng:
- Chỉ có một trục đối xứng dọc: A, M, T, U, V, Y
- Chỉ có một trục đối xứng ngang: B, C, D, Đ, E, K
- Có hai trục đối xứng dọc và ngang: H, I, O, X
b) Có thế gấp tờ giấy làm tư để cắt chữ H vì chữ H có hai trục đối xứng vuông góc.
a) Cắt được chữ D với nét gấp là trục đối xứng ngang của chữ D.
Các chữ cái có trục đối xứng:
- Chỉ có một trục đối xứng dọc: A, M, T, U, V, Y
- Chỉ có một trục đối xứng ngang: B, C, D, Đ, E, K
- Có hai trục đối xứng dọc và ngang: H, I, O, X
b) Có thế gấp tờ giấy làm tư để cắt chữ H vì chữ H có hai trục đối xứng vuông góc.

Bài giải:
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
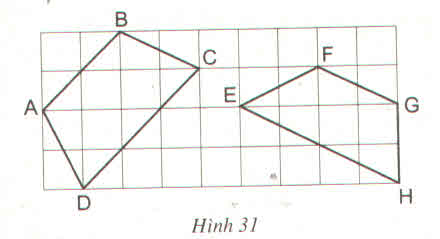
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.

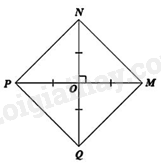
Vì \(OM = ON = OP = OQ\) nên \(O\) là trung điểm của \(NQ\) và \(MP\) và \(MP = NQ\)
Xét tứ giác \(MNPQ\) có hai đường chéo \(NQ\) và \(MP\) cắt nhau tại trung điểm \(O\) (cmt)
Suy ra \(MNPQ\) là hình bình hành
Mà \(MP = NQ\) (cmt) nên \(MNPQ\) là hình chữ nhật
Lại có \(MP \bot NQ\) (gt) nên \(MNPQ\) là hình vuông

- Trong trường hợp a:
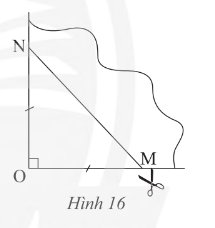
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.

Các bước làm như sau:
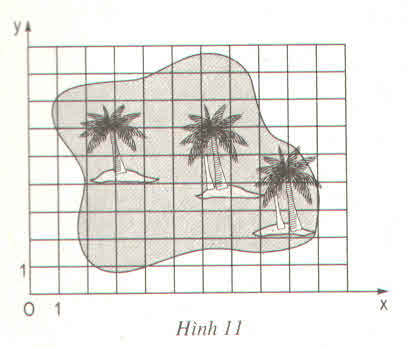
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
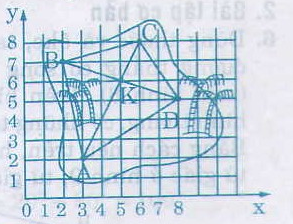
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ.
Bài giải:
Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 
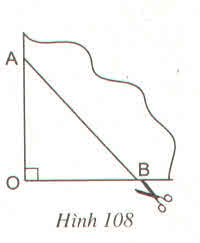
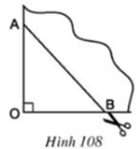
Tứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.