Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

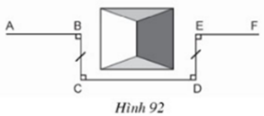
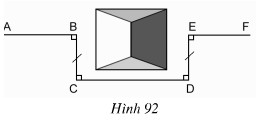
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD);
BC = DE
nên BCDE là hình bình hành ⇒ CD // BE.
Lại có : 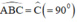 ⇒ AB // CD
⇒ AB // CD
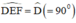 ⇒ EF // CD
⇒ EF // CD
Theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.

Xét tứ giác BEDC có:
BC // ED (vì cùng ⊥⊥ CD)
BC = ED (gt)
Nên BEDC là hình bình hành.
Hình bình hành BEDC có \(\widehat{C}=90^o\) nên BEDC là hình chữ nhật.
\(\Rightarrow\widehat{CBE}=\widehat{BED}=90^o\)
Khi đó \(\widehat{ABC}+\widehat{CBE}=180^o\) \(\Rightarrow\) A, B, E thẳng hàng.
\(\widehat{BED}+\widehat{DEF}=180^o\Rightarrow\) B, E, F thẳng hàng.
Vậy AB và EF cùng nằm trên một đường thẳng.

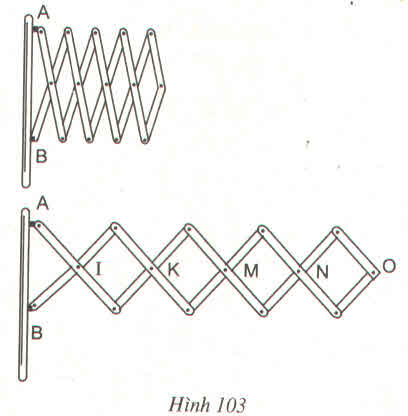
78. Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bàng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng ?
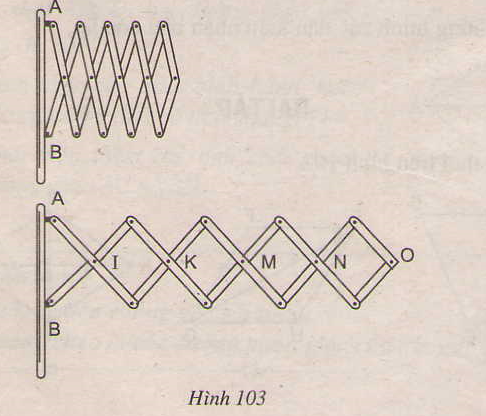
Bài giải:
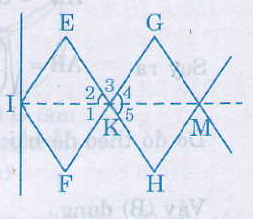
Các tứ giác IEKF, KGMH là hình thoi nên KI là phân giác góc EKF, KM là phân giác của góc GKH.
Mà ˆEKFEKF^ = ˆHKGHKG^
Nên ˆK1K1^ = ˆK2K2^ = ˆK4K4^ = ˆK5K5^
Do đó ˆK2K2^ +ˆK3K3^ + ˆK4K4^ = ˆK2K2^ + ˆK3K3^ + ˆK1K1^=1800
Suy ra I, K, M thẳng hàng.
Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.

Các tứ giác IEKF, KGMH là hình thoi nên KI là phân giác góc EKF, KM là phân giác của góc GKH.
Mà ˆEKFEKF^ = ˆHKGHKG^
Nên ˆK1K1^ = ˆK2K2^ = ˆK4K4^ = ˆK5K5^
Do đó ˆK2K2^ +ˆK3K3^ + ˆK4K4^ = ˆK2K2^ + ˆK3K3^ + ˆK1K1^=1800
Suy ra I, K, M thẳng hàng.
Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.

Bài giải:
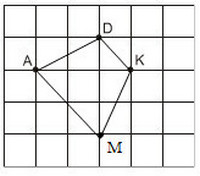
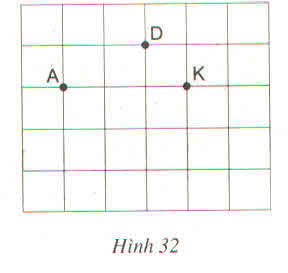
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).

Bài giải:
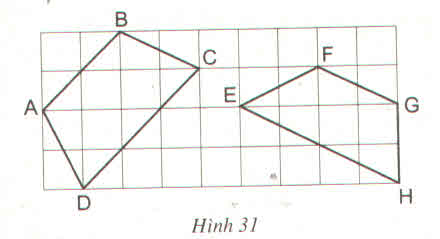
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.

Bài giải:
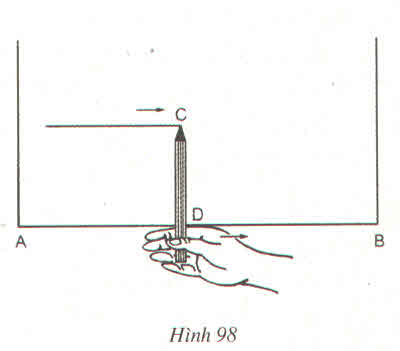
Căn cứ vào tính chất đưởng thẳng song song với một đường thẳng cho trước ta kết luận là vì điểm C cách mép gỗ AB một khoảng bằng 10cm nên đầu chì C vạch nên đường thằng song song với AB và cách AB một khoảng 10cm.
Căn cứ vào tính chất đưởng thẳng song song với một đường thẳng cho trước ta kết luận là vì điểm C cách mép gỗ AB một khoảng bằng 10cm nên đầu chì C vạch nên đường thằng song song với AB và cách AB một khoảng 10cm.

Bài giải:
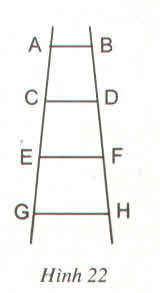
Có tất cả 6 hình thang, đó là: ABDC, CDFE, EFHG, ABFE, CDHG, ABHG

Các bước làm như sau:
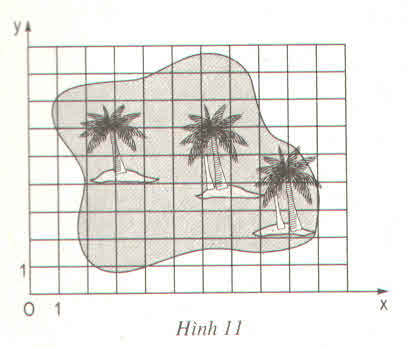
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
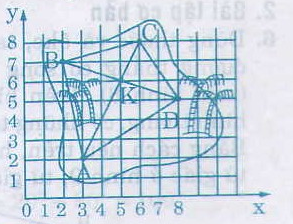
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ.
Bài giải:
Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 
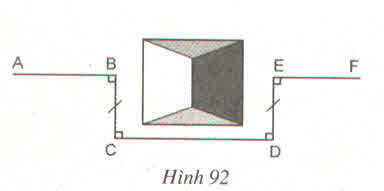
Bài giải:
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD)
BC = DE
nên BCDE là hình chữ nhật
Do đó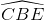 = 900 ,
= 900 , 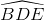 = 900
= 900
Suy ra AB và EF cùng nằm trên một đường thẳn