Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

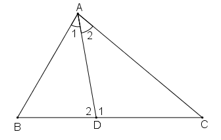
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o

a, xét tam giác ABD, tam giác HBD có
AB=BH ;góc ABD= góc HBD ( vì phân giác) ,BD chung
suy ra 2 tam giác bằng nhau theo trường hợp cạnh góc cạnh
b, vì 2 tam giác bằng nhau ( câu a) suy ra góc BAD= góc BDH mà BAD= 90 độ suy ra BHD =90 độ hay DH vuông góc với BC
C, nếu góc C =60 độ suy ra góc B = 0 độ suy ra góc ABD= 15 độ suy ra góc ADB = 90 độ -15 độ = 75 độ ( phụ nhau)

B2 : Hình dễ bạn tử kẻ hình nhá !
a)Ta có AH là đường cao
=> Góc AHB = AHC = 90o
Xết tam giác AHB có :
BAH + AHB + HBA = 180o ( tổng 3 góc trong 1 tam giác )
=> BAH + 90o + 70o =180o
=> BAH = 180o-70o-90o
=> BAH = 20o
Xét tam giác AHC cps :
AHC + HAC + HCA = 180o
=> 90 + HAC + 30 = 180
=> HAC = 180-30-90=60o
b) Ta có AD là đường phân giác
=> ABD= CAD = 80/2 = 40o
Xét tam giác ADB có :
ABD + BDA +DAB = 180
=> 70 + BDA + 40 = 180
=> BDA = 180-40-70 = 70
Xét tam giác ADC có :
ACD + CDA + DAC = 180
=> 30 + CDA + 40 = 180
=> CDA = 180-40-30
=> CDA=110
( **** )

Giải
Ta có: tam giác ABC: A + B + C = 180 ( định lý )
60 + B + 50 = 180
B + 110 = 180
B = 180 - 110
B = 70
Ta có: B = B1 + B2 ( theo hình mk vẽ và đặt tên)
=> B = 70 => B1 = B2 = 35
Ta có: B1 + A = ADB ( t chất góc ngoài )
35 + 60 = ADB
=> ADB = 95
Mặt khác B2 + C = BDC ( T chất góc ngoài )
35 + 50 = BDC
=> BDC = 85
Vậy .......
Thêm dấu góc nha, mk

Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)
Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)
\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)
\(\Leftrightarrow a-b=-20\)
mà a+b=180
nên 2a=160
=>a=80
=>b=100