Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
#Học tốt!!!
\(ab\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{ab}\)
\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)
\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)
\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)

a) \(\sqrt{\dfrac{1}{600}}=\dfrac{\sqrt{1}}{10\sqrt{6}}=\dfrac{\sqrt{1}.\sqrt{6}}{10\sqrt{6}.\sqrt{6}}=\dfrac{\sqrt{6}}{60}\)
b) \(\sqrt{\dfrac{11}{540}}=\dfrac{\sqrt{11}}{6\sqrt{15}}=\dfrac{\sqrt{11}.\sqrt{15}}{6\sqrt{15}.\sqrt{15}}=\dfrac{\sqrt{165}}{90}\)
c) \(\sqrt{\dfrac{3}{50}}=\dfrac{\sqrt{3}}{5\sqrt{2}}=\dfrac{\sqrt{3}.\sqrt{2}}{5\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{6}}{10}\)
d) \(\sqrt{\dfrac{5}{98}}=\dfrac{\sqrt{5}}{7\sqrt{2}}=\dfrac{\sqrt{5}.\sqrt{2}}{7\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{10}}{14}\)
e) \(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{\sqrt{\left(1-\sqrt{3}\right)^2}}{3\sqrt{3}}=\dfrac{\sqrt{3}-1}{3\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{3\sqrt{3}.\sqrt{3}}=\dfrac{3-\sqrt{3}}{9}\)
\(\sqrt{\dfrac{1}{600}}=\sqrt{\dfrac{1\cdot6}{600\cdot6}}=\sqrt{\dfrac{6}{60^2}}=\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}=\sqrt{\dfrac{11\cdot15}{540\cdot15}}=\sqrt{\dfrac{165}{90^2}}=\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}=\sqrt{\dfrac{3\cdot2}{50\cdot2}}=\sqrt{\dfrac{6}{10^2}}=\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}=\sqrt{\dfrac{5\cdot2}{98\cdot2}}=\sqrt{\dfrac{10}{12^2}}=\dfrac{\sqrt{10}}{12}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\sqrt{\dfrac{3\left(1-\sqrt{3}\right)^2}{27\cdot3}}\)
\(=\dfrac{\sqrt{3\left(1-\sqrt{3}\right)^2}}{\sqrt{9^2}}=\dfrac{\left|1-\sqrt{3}\right|\cdot\sqrt{3}}{9}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\sqrt{3}}{9}\)

\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{5}{2\sqrt{5}}=\frac{10\sqrt{5}}{20}=\frac{\sqrt{5}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{3\sqrt{20}}{180}=\frac{\sqrt{20}}{60}=\frac{2\sqrt{5}}{60}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{10\sqrt{2}\left(\sqrt{2}+1\right)}{50}=\frac{20+10\sqrt{2}}{50}=\frac{10\left(2+\sqrt{2}\right)}{50}=\frac{2+\sqrt{2}}{5}\)
\(\frac{y+b\sqrt{y}}{b\sqrt{y}}=\frac{y\left(\sqrt{y}+b\right)}{by}=\frac{\sqrt{y}+b}{b}\)
+ Ta có:
5√10=5.√10√10.√10=5√10(√10)2=5√1010510=5.1010.10=510(10)2=51010
=5.√105.2=5.105.2=√102=102.
+ Ta có:
52√5=5.√52√5.√5=5√52.(√5.√5)=5√52(√5)2525=5.525.5=552.(5.5)=552(5)2
=5√52.5=√52=552.5=52.
+ Ta có:
13√20=1.√203√20.√20=√203.(√20.√20)=√203.(√20)21320=1.20320.20=203.(20.20)=203.(20)2
=√203.20=√22.560=2√560=2√52.30=√530=203.20=22.560=2560=252.30=530.
+ Ta có:
(2√2+2)5.√2=(2√2+2).√25√2.√2=2√2.√2+2.√25.(√2)2(22+2)5.2=(22+2).252.2=22.2+2.25.(2)2
=2.2+2√25.2=2(2+√2)5.2=2+√25=2.2+225.2=2(2+2)5.2=2+25.
+ Ta có:
y+b√yb√y=(y+b√y).√yb√y.√y=y√y+b√y.√yb.(√y)2y+byby=(y+by).yby.y=yy+by.yb.(y)2
=y√y+b(√y)2by=y√y+byby=yy+b(y)2by=yy+byby
=y(√y+b)b.y=√y+bb=y(y+b)b.y=y+bb.
Cách khác:
y+b√yb√y=(√y)2+b√yb√yy+byby=(y)2+byby=√y(√y+b)b√y=√y+bb
Nguồn : Bài 50 trang 30 SGK Toán 9 tập 1 - loigiaihay.com
#Ye Chi-Lien

+ Ta có:
2√6−√5=2(√6+√5)(√6−√5)(√6+√5)26−5=2(6+5)(6−5)(6+5)
=2(√6+√5)(√6)2−(√5)2=2(√6+√5)6−5=2(6+5)(6)2−(5)2=2(6+5)6−5
=2(√6+√5)1=2(√6+√5)=2(6+5)1=2(6+5).
+ Ta có:
3√10+√7=3(√10−√7)(√10+√7)(√10−√7)310+7=3(10−7)(10+7)(10−7)
=3(√10−√7)(√10)2−(√7)2=3(10−7)(10)2−(7)2=3(√10−√7)10−7=3(10−7)10−7
=3(√10−√7)3=√10−√7=3(10−7)3=10−7.
+ Ta có:
1√x−√y=1.(√x+√y)(√x−√y)(√x+√y)1x−y=1.(x+y)(x−y)(x+y)
=√x+√y(√x)2−(√y)2=√x+√yx−y=x+y(x)2−(y)2=x+yx−y
+ Ta có:
2ab√a−√b=2ab(√a+√b)(√a−√b)(√a+√b)2aba−b=2ab(a+b)(a−b)(a+b)
=2ab(√a+√b)(√a)2−(√b)2=2ab(√a+√b)a−b=2ab(a+b)(a)2−(b)2=2ab(a+b)a−b.
\(\frac{2}{\sqrt{6}-\sqrt{5}}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)
\(\frac{3}{\sqrt{10}+\sqrt{7}}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}-\sqrt{7}\right)\left(\sqrt{10}+\sqrt{7}\right)}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\sqrt{10}-\sqrt{7}\)
\(\frac{1}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\frac{2ab}{\sqrt{a}-\sqrt{b}}=\frac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)

+ Ta có:
3√3+1=3(√3−1)(√3+1)(√3−1)=3√3−3.1(√3)2−1233+1=3(3−1)(3+1)(3−1)=33−3.1(3)2−12
=3√3−33−1=3√3−32=33−33−1=33−32.
+ Ta có:
2√3−1=2(√3+1)(√3−1)(√3+1)=2(√3+1)(√3)2−1223−1=2(3+1)(3−1)(3+1)=2(3+1)(3)2−12
=2(√3+1)3−1=2(√3+1)2=√3+1=2(3+1)3−1=2(3+1)2=3+1.
+ Ta có:
2+√32−√3=(2+√3).(2+√3)(2−√3)(2+√3)=(2+√3)222−(√3)22+32−3=(2+3).(2+3)(2−3)(2+3)=(2+3)222−(3)2
=22+2.2.√3+(√3)24−3=22+2.2.3+(3)24−3=4+4√3+31=(4+3)+4√31=4+43+31=(4+3)+431
=7+4√31=7+4√3=7+431=7+43.
+ Ta có:
b3+√b=b(3−√b)(3+√b)(3−√b)b3+b=b(3−b)(3+b)(3−b)
=b(3−√b)32−(√b)2=b(3−√b)9−b;(b≠9)=b(3−b)32−(b)2=b(3−b)9−b;(b≠9).
+ Ta có:
p2√p−1=p(2√p+1)(2√p−1)(2√p+1)p2p−1=p(2p+1)(2p−1)(2p+1)
=p(2√p+1)(2√p)2−12=p(2√p+1)4p−1=p(2p+1)(2p)2−12=p(2p+1)4p−1=2p√p+p4p−1
Bài 51 trang 30 SGK Toán 9 tập 1 - loigiaihay.com
#Ye Chi-Lien
\(\frac{3}{\sqrt{3}+1}=\frac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\frac{3\sqrt{3}-3}{3-1}=\frac{3\sqrt{3}-3}{2}\)
\(\frac{2}{\sqrt{3}-1}=\frac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\frac{2\left(\sqrt{3}+1\right)}{3-1}=\sqrt{3}-1\)
\(\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{\left(2+\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3}=\left(2+\sqrt{3}\right)^2=4+4\sqrt{3}+3=7+4\sqrt{3}\)
\(\frac{b}{3+\sqrt{b}}=\frac{b\left(3-\sqrt{b}\right)}{\left(3+\sqrt{b}\right)\left(3-\sqrt{b}\right)}=\frac{b\left(3-\sqrt{b}\right)}{9-b}\)
\(\frac{p}{2\sqrt{p}-1}=\frac{p\left(2\sqrt{p}+1\right)}{\left(2\sqrt{p}-1\right)\left(2\sqrt{b}+1\right)}=\frac{p\left(2\sqrt{b}+1\right)}{4p-1}\)

1) Ta có: \(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
\(=3\cdot2\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{3}+2\sqrt{3}-3\sqrt{3}\)
\(=5\sqrt{3}\)
2) Ta có: \(\dfrac{2}{\sqrt{3}-5}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{\left(\sqrt{3}-5\right)\left(\sqrt{3}+5\right)}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{3-25}\)
\(=\dfrac{-2\left(\sqrt{3}+5\right)}{22}\)
\(=\dfrac{-\sqrt{3}-5}{11}\)
3) Ta có: \(\sqrt{\dfrac{2}{5}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{2}\cdot\sqrt{5}}{5}\)
\(=\dfrac{\sqrt{10}}{5}\)
Nếu em thấy các câu hỏi do lag mà bị gửi đúp (tức là rất nhiều câu hỏi giống nhau xuất hiện cùng 1 chỗ) thì xóa giúp mình nhé cho đỡ vướng. Nhưng nhớ để lại 1 câu. Cảm ơn em.

LG a
12√48−2√75−√33√11+5√1131248−275−3311+5113;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
12√48−2√75−√33√11+5√1131248−275−3311+5113
=12√16.3−2√25.3−√3.11√11+5√1.3+13=1216.3−225.3−3.1111+51.3+13
=12√42.3−2√52.3−√3.√11√11+5√43=1242.3−252.3−3.1111+543
=12.4√3−2.5√3−√3+5√4√3=12.43−2.53−3+543
=42√3−10√3−√3+5√4.√3√3.√3=423−103−3+54.33.3
=2√3−10√3−√3+52√33=23−103−3+5233
=2√3−10√3−√3+10√33=23−103−3+1033
=(2−10−1+103)√3=(2−10−1+103)3
=−173√3=−1733.
LG b
√150+√1,6.√60+4,5.√223−√6;150+1,6.60+4,5.223−6;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
√150+√1,6.√60+4,5.√223−√6150+1,6.60+4,5.223−6
=√25.6+√1,6.60+4,5.√2.3+23−√6=25.6+1,6.60+4,5.2.3+23−6
=√52.6+√1,6.(6.10)+4,5√83−√6=52.6+1,6.(6.10)+4,583−6
=5√6+√(1,6.10).6+4,5√8√3−√6=56+(1,6.10).6+4,583−6
=5√6+√16.6+4,5√8.√33−√6=56+16.6+4,58.33−6
=5√6+√42.6+4,5√8.33−√6=56+42.6+4,58.33−6
=5√6+4√6+4,5.√4.2.33−√6=56+46+4,5.4.2.33−6
=5√6+4√6+4,5.√22.63−√6=56+46+4,5.22.63−6
=5√6+4√6+4,5.2√63−√6=56+46+4,5.263−6
=5√6+4√6+9√63−√6=56+46+963−6
=5√6+4√6+3√6−√6=56+46+36−6
=(5+4+3−1)√6=11√6.=(5+4+3−1)6=116.
Cách 2: Ta biến đổi từng hạng tử rồi thay vào biểu thức ban đầu:
+ √150=√25.6=5√6150=25.6=56
+ √1,6.60=√1,6.(10.6)=√(1,6.10).6=√16.61,6.60=1,6.(10.6)=(1,6.10).6=16.6
=4√6=46
+ 4,5.√223=4,5.√2.3+23=4,5.√83=4,5√8.334,5.223=4,5.2.3+23=4,5.83=4,58.33
=4,5.√4.2.33=4,5.2.√63=9.√63=3√6.=4,5.4.2.33=4,5.2.63=9.63=36.
Do đó:
√150+√1,6.√60+4,5.√223−√6150+1,6.60+4,5.223−6
=5√6+4√6+3√6−√6=56+46+36−6
=(5+4+3−1)√6=11√6=(5+4+3−1)6=116
LG c
(√28−2√3+√7)√7+√84;(28−23+7)7+84;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Hằng đẳng thức số 1: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
=(√28−2√3+√7)√7+√84=(28−23+7)7+84
=(√4.7−2√3+√7)√7+√4.21=(4.7−23+7)7+4.21
=(√22.7−2√3+√7)√7+√22.21=(22.7−23+7)7+22.21
=(2√7−2√3+√7)√7+2√21=(27−23+7)7+221
=2√7.√7−2√3.√7+√7.√7+2√21=27.7−23.7+7.7+221
=2.(√7)2−2√3.7+(√7)2+2√21=2.(7)2−23.7+(7)2+221
=2.7−2√21+7+2√21=2.7−221+7+221
=14−2√21+7+2√21=14−221+7+221
=14+7=21=14+7=21.
LG d
(√6+√5)2−√120.(6+5)2−120.
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Hằng đẳng thức số 1: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
Lời giải chi tiết:
Ta có:
(√6+√5)2−√120(6+5)2−120
=(√6)2+2.√6.√5+(√5)2−√4.30=(6)2+2.6.5+(5)2−4.30
=6+2√6.5+5−2√30=6+26.5+5−230
=6+2√30+5−2√30=6+5=11.=6+230+5−230=6+5=11.

\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{2-1}=2\sqrt{2}-2+2-\sqrt{2}=\sqrt{2}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\)
\(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
\(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}=\dfrac{\left(a-\sqrt{a}\right)\left(1+\sqrt{a}\right)}{1-a}=\dfrac{a+a\sqrt{a}-\sqrt{a}-a}{1-a}=\dfrac{\sqrt{a}\left(a-1\right)}{1-a}=-\sqrt{a}\)
\(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
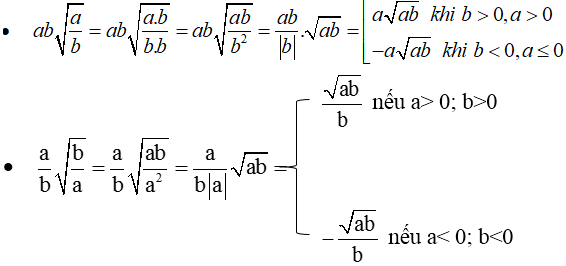

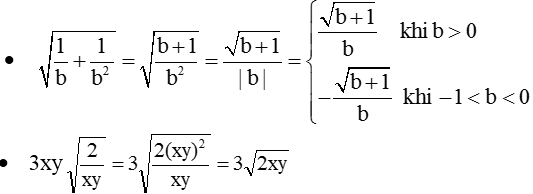
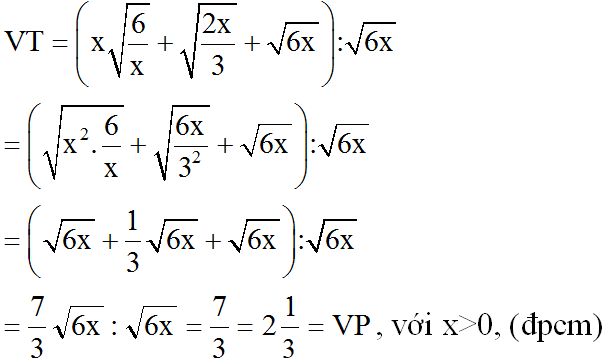
\(\sqrt{\dfrac{1}{600}}\)=\(\sqrt{\dfrac{1}{10^2\cdot6}}\)=\(\sqrt{\dfrac{1\cdot6}{10^2\cdot6\cdot6}}\)=\(\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}\)=\(\sqrt{\dfrac{11\cdot540}{540\cdot540}}\)=\(\dfrac{\sqrt{5940}}{540}\)=\(\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}\)=\(\sqrt{\dfrac{3\cdot50}{50\cdot50}}\)=\(\dfrac{\sqrt{150}}{50}\)=\(\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}\)=\(\sqrt{\dfrac{5\cdot98}{98\cdot98}}=\dfrac{\sqrt{490}}{98}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)
\(\sqrt{\dfrac{1}{600}}=\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}=\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}=\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)