Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
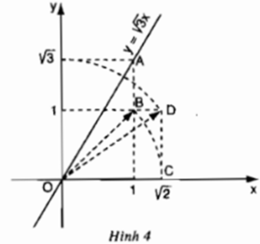
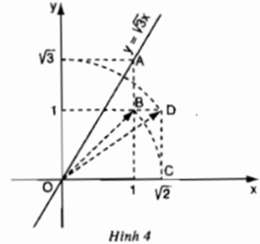
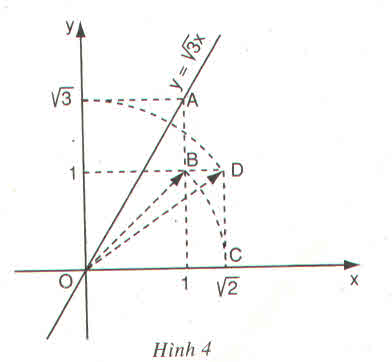
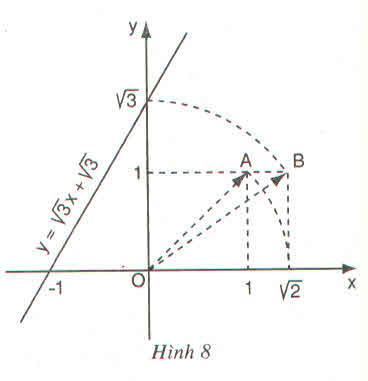
+ Dựng điểm B(1; 1). Vẽ OB ta được
![]()
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
![]()
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.

- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
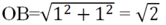
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
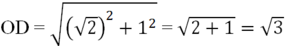
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.

Ta có: \(\sqrt{3}\) = \(\sqrt{2+1}\) = \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)
Hình vẽ SGK có : OC = OB = \(\sqrt{2}\) và theo định lí Py-ta-go t a có :
OD = \(\sqrt{OC^2+CD^2}\)= \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)= \(\sqrt{3}\)
Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A.
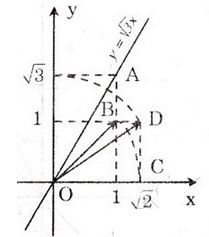

Bài giải:
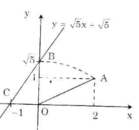
Hình bên diễn tả cách dựng đoạn thẳng có độ dài bằng √5.
Đồ thị hàm số y = √5 x + √5 đi qua hai điểm A(0; √5) và B(-1; 0).
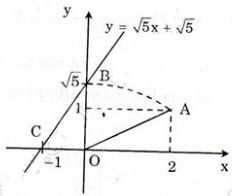

Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
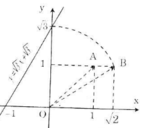
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

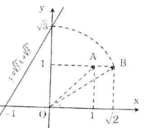
a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
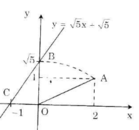
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

Lời giải:
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
b) - Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
a) Tự vẽ đths :vvv
ĐTHS y = 2x là đường thẳng đi qua (0;0) và (2;1)
ĐTHS y = -2x là đường thẳng đi qua (0;0) và (-2;1)
b) Xét 2 hàm số:
Vì h/s y = 2x có 2 > 0 => HS đồng biến
Vì h/s y = -2x có -2 < 0 => HS nghịch biến
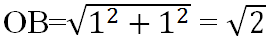
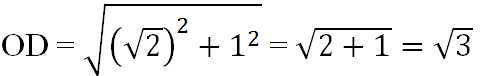

Cách vẽ:
- Cho x=1x=1 ta được y=√3.1=√3y=3.1=3. Suy ra A(1;√3)A(1;3)
- Cho x=0x=0 ta được y=√.0=0y=.0=0. Suy ra O(0;0)O(0;0)
Vẽ đường thẳng qua O, A được đồ thị hàm số y=√3x.y=3x.
Các bước vẽ:
- Vẽ một hình vuông có độ dài cạnh là 1 đơn vị, có một đỉnh là O, lấy điểm B(1;1)B(1;1). Khi đó, đường chéo OB có độ dài bằng √12+12=√2.12+12=2.
- Vẽ cung tròn tâm OO, bán kính OBOB , ta xác định được điểm CC trên tia OxOx, và ta có OC=√2.OC=2.
- Vẽ một hình chữ nhật có một đỉnh là O, cạnh CD = 1 và cạnh OC = OB = √22 ta được đường chéo OD=√CD2+OC2=√1+(√2)2=√3.OD=CD2+OC2=1+(2)2=3.
- Vẽ cung tròn tâm OO, bán kính ODOD , ta xác định được điểm EE trên tia OyOy, và ta có OE=√3.OE=3.
- Vẽ hình chữ nhật có một đỉnh là O, có một cạnh bằng 1 đơn vị và một cạnh có độ dài bằng OE=√3OE=3 ta được điểm A(1;√3)A(1;3) .
- Vẽ đường thẳng đi qua gốc tọa độ O và điểm A ta được đồ thị của hàm số y=√3xy=3x
+,vẽ hình vuông có đọ dài cạch lá 1đon vị,một đỉnh lá O,ta được đường chéo OB có độ dài =\(\sqrt{2}\)
+,vẽ hình chữ nhạt có 1 đỉnh là O, cạnh CD=1 và cạnh OC=\(\sqrt{2}\),ta được đường chéo ODcó độ dài=\(\sqrt{3}\).
+.vẽ hình chữ nhật có một đỉnh O,một cạnh =1 và 1 cạch =\(\sqrt{3}\),ta được điểm A (1,\(\sqrt{3}\))
+vẽ dduongf thẳng qua góc tọa độ Ovà điểm A ta dduocjw ddof thị của hàm số y=\(\sqrt{3}\)x