Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khai phương tích :
\(\sqrt{12\cdot30\cdot40}=\sqrt{3\cdot4\cdot3\cdot10\cdot4\cdot10}=\sqrt{3^2\cdot4^2\cdot10^2}=3\cdot4\cdot10=120\)
Vậy đáp án B-120 đúng.
câu b đúng .
\(\sqrt{12}\cdot\sqrt{30}\cdot\sqrt{40}\) = \(\sqrt{12\cdot30\cdot40}\) = \(120\)
nên câu b đúng

a, \(\sqrt{0.09\cdot64=\sqrt{0.09}\cdot\sqrt{64}=0.3\cdot8=2.4}\)
b, \(\sqrt{2^4\cdot\left(-7\right)^2}=\sqrt{16\cdot49}=\sqrt{16}\cdot\sqrt{49}=4\cdot7=28\)
c, \(\sqrt{121\cdot360}=\sqrt{121\cdot36}=\sqrt{121}\cdot\sqrt{36}=11\cdot6=66\)
d, \(\sqrt{2^2\cdot3^4}=\sqrt{2^2}\cdot\sqrt{3^4}=2\cdot3^2=18\)
a)\(\sqrt{0,09}.\sqrt{64}\)=0,3.8=2,4
b)\(\sqrt{2^4}.\sqrt{\left(-7\right)^2}\)=4.7=28
c)\(\sqrt{121.36}\)=\(\sqrt{121}.\sqrt{36}\)=11.6=66
d)\(\sqrt{2^2}.\sqrt{3^4}\)=2.9=18

Ta có:
12+√3+12−√312+3+12−3
=2−√3(2+√3)(2−√3)+2+√3(2−√3)(2+√3)=2−3(2+3)(2−3)+2+3(2−3)(2+3)
=2−√322−(√3)2+2+√322−(√3)2=2−322−(3)2+2+322−(3)2
=2−√34−3+2+√34−3=2−34−3+2+34−3
=2−√31+2+√31=2−31+2+31
=2−√3+2+√3=4=2−3+2+3=4.
Chọn đáp án (D). 44
Ta có : \(\frac{1}{2+\sqrt{3}}+\frac{1}{2-\sqrt{3}}=\frac{2-\sqrt{3}+2+\sqrt{3}}{4-3}=4\)
Vậy chọn D

a) \(\sqrt{13^2-12^2}\)=\(\sqrt{\left(13-12\right)\left(13+12\right)}\)=\(\sqrt{1x25}\)=5
Câu a: Ta có:
√132−122=√(13+12)(13−12)132−122=(13+12)(13−12)
=√25.1=√25=25.1=25
=√52=|5|=5=52=|5|=5.
Câu b: Ta có:
√172−82=√(17+8)(17−8)172−82=(17+8)(17−8)
=√25.9=√25.√9=25.9=25.9
=√52.√32=|5|.|3|=52.32=|5|.|3|.
=5.3=15=5.3=15.
Câu c: Ta có:
√1172−1082=√(117−108)(117+108)1172−1082=(117−108)(117+108)
=√9.225=9.225 =√9.√225=9.225
=√32.√152=|3|.|15|=32.152=|3|.|15|
=3.15=45=3.15=45.
Câu d: Ta có:
√3132−3122=√(313−312)(313+312)3132−3122=(313−312)(313+312)
=√1.625=√625=1.625=625
=√252=|25|=25=252=|25|=25.

Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 11cm. Diện tích của tam giác ABCABC bằng:
A. \(6cm^2\) ; B. \(\sqrt{3}cm^2\) ;
C.\(\frac{3\sqrt{3}}{4}cm^2\) ; D. \(3\sqrt{3cm^2}\)
Câu trả lời đúng là D.
Gọi OO là tâm đường tròn nội tiếp tam giác đều ABCABC, HH là tiếp điểm thuộc BCBC.
Đường phân giác AOAO của góc AA cũng là đường cao nên AA, OO, HH thẳng hàng.
\mathrm{HB}=\mathrm{HC}HB=HC, \widehat{HAC}=30^{\circ}HAC=30∘
AH=3\cdot OH=3AH=3⋅OH=3(cm)
HC=AH \cdot tan 30^{\circ}=3 \cdot \dfrac{1}{\sqrt{3}}=\sqrt{3}HC=AH⋅tan30∘=3⋅31=3(cm)
S_{ABC}=\dfrac{1}{2} BC.AH=HC.AH=3 \sqrt{3}SABC=21BC.AH=HC.AH=33(cm^{2}2)
Vì thế, câu trả lời (D) là đúng.

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Xét trong đường tròn nhỏ:
Theo định lí 22: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết AB>CDAB>CD suy ra ABAB gần tâm hơn, tức là OH<OKOH<OK.
b) Xét trong đường tròn lớn:
Theo định lí 22: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu aa, ta có: OH<OK⇒ME>MFOH<OK⇒ME>MF.
c) Xét trong đường tròn lớn:
Vì OH⊥ME⇒EH=MH=ME2OH⊥ME⇒EH=MH=ME2 (Định lý 2 - trang 103).
Vì OK⊥MF⇒KF=MK=MF2OK⊥MF⇒KF=MK=MF2 (Định lý 2 - trang 103).
Theo câu bb, ta có: ME>MF⇒ME2>MF2⇔MH>MK

a, \(x^2-5=0\Leftrightarrow\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)=0\Leftrightarrow x=\pm\sqrt{5}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{\pm\sqrt{5}\right\}\)
b, \(x^2-2\sqrt{11}x+11=0\Leftrightarrow x^2-2\sqrt{11}x+\left(\sqrt{11}\right)^2=0\)
\(\Leftrightarrow\left(x-\sqrt{11}\right)^2=0\Leftrightarrow x=\sqrt{11}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\sqrt{11}\right\}\)
x2 - 5 = 0
Δ = b2 - 4ac = 0 + 20 = 20
Δ > 0, áp dụng công thức nghiệm thu được x = ±√5
x2 - 2√11x + 11 = 0
Δ = b2 - 4ac = 44 - 44 = 0
Δ = 0 => phương trình có nghiệm kép x1 = x2 = -b/2a = √11
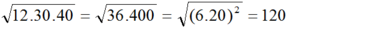
Khai phương tích 12.30.40 được:
(A) 1200 ; (B) 120 ; (C) 12 ; (D) 240.
Chọn B
Khai phương tích 12.30.40 (=12.12.10.10) ta được 12.10= 120 (Chọn B)