Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) nối A với C , B với D được:
EF // AC ( đường trung bình của tam giác BAC)
HG // AC ( " " " " " " ) suy ra EF // AC do cùng // AC
HE // DB ( đường trung bình tam giác ADB )
FG // DB ( " " " " " " ) suy ra HE // FG do cùng // với DB
Xét tứ giác EFGH có 2 cặp cạnh đối song song nên EFGH là hình bình hành
b) EFGH là hình ....
Thoi , suy ra EH = GH nên AC=BD ( do là đường trung bình của hai tam giác ADB,ADC)
vì AC = BD nên ABCD là hình thang cân
Chữ nhật, suy ra HE vuông góc với HG nên AC vuông góc với BD
Hình vuông , kết hợp 2 yếu tố của 2 hình trên được AC=BD và AC vuông góc với BD.
Tích nha☺

A
BCDFEOa, Vì tứ giác ABCD là hình hình hành
⇒ ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪AD // BCAD = BC AB = CDAB // CD{AD // BCAD = BC AB = CDAB // CD
Vì AD // BC
⇒ AD // BE
Vì {AD = BCBE= BC{AD = BCBE= BC
⇒ AD = BE
Tứ giác EADB có
{AD // BEAD = BE{AD // BEAD = BE
⇒ Tứ giác EADB là hình bình hành (đpcm)
b, Vì tứ giác EADB là hình bình hành
⇒ AE // BD (1)
Vì {AB = CDDF = CD{AB = CDDF = CD
⇒ AB = DF
Vì AB // CD
⇒ AB // DF
Tứ giác ABDF có
{AB = DFAB // DF{AB = DFAB // DF
⇒ Tứ giác ABDF là hình bình hành
⇒ AF // BD (2)
Từ (1), (2) ⇒ E, A và F thẳng hàng (đpcm)
c, Vì tứ giác EADB là hình bình hành
⇒ AE = BD (3)
Vì tứ giác ABDF là hình bình hành
⇒ AF = BD (4)
Từ (3), (4) ⇒ AE = AF
Vì {AE = AFE, A, F thẳng hàng {AE = AFE, A, F thẳng hàng
⇒ A là trung điểm của EF
⇒ CA là đường trung tuyến của ΔCEF
Vì DC = DF
⇒ D là trung điểm của EF
⇒ ED là đường trung tuyến của ΔCEF
Vì BE = BC
⇒ B là trung điểm của EC
⇒ FB là đường trung tuyến của ΔCEF
Như vậy
⎧⎩⎨⎪⎪CA là đường trung tuyến của ΔCEF ED là đường trung tuyến của ΔCEFFB là đường trung tuyến của ΔCEF{CA là đường trung tuyến của ΔCEF ED là đường trung tuyến của ΔCEFFB là đường trung tuyến của ΔCEF
⇒ CA, ED, FB đồng quy (tại trọng tâm của ΔCEF) (đpcm)
học tốt ;-;

A B C D E F M N I
Ta có AECF là hình bình hành=> EF cắt AC ở trung điểm I của mỗi đường
AMCN là hình bình hành=>MN cắt AC ở trung điểm của mỗi đường
=>EF cắt MN ở trung điểm mỗi đường=> ĐPCM

Tự vẽ hình
a) Ta có: AB = CD (cạnh hình thoi)
BE = DG (g.t)
=> AB + BE = CD + DG hay AE = CG (cmt)
Xét tam giác AHE và tam giác CFG ta có:
AE=CG
HAE = FCG (cùng bù vs BAD = DCB)
AH=CF (gt)
Do đó tam giác AHE = tam giác CFG (c.g.c) => HE = FG
Do đó EFGH là cạnh bình hành (đpcm)
b) Nối E vs G
Xét tam giác OBE và tam giác ODG ta có:
BE= DG (gt)
OBE = ODG (so le trong)
OB = OD ( tính chất đường chéo của hình thoi ABCD)
=> tam giác OBE = tam giác ODG (c.g.c) => OBE = ODG
Mà DOG + GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
\(\Leftrightarrow\Delta HAE=\Delta EBF\left(c.c.c\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EBF}=\widehat{EDA}\left(đv\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}\) mà \(\widehat{HAE}+\widehat{EAD=180^O\left(kb\right)}\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}=90^O\)
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
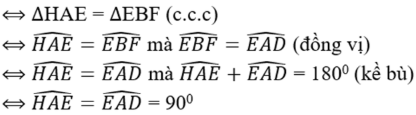
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.