Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

– Sử dụng hàm sum để tính tổng và điểm trung bình.
- Gọi hàm Python thực hiện sắp xếp thứ tự tăng dần (không giảm); sau khi sắp xếp thì tìm được ngay max, min.
- Dãy số đã sắp thứ tự tăng dần (không giảm) nên có thể dùng hàm bisect left (trong mô đun bisect) tìm được các vị trí phân chia dãy điểm thành 4 đoạn điểm: Chưa đạt, Đạt, Khá và Tốt. Từ đó tính được số lượng điểm theo từng mức xếp hạng.


a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:
- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5
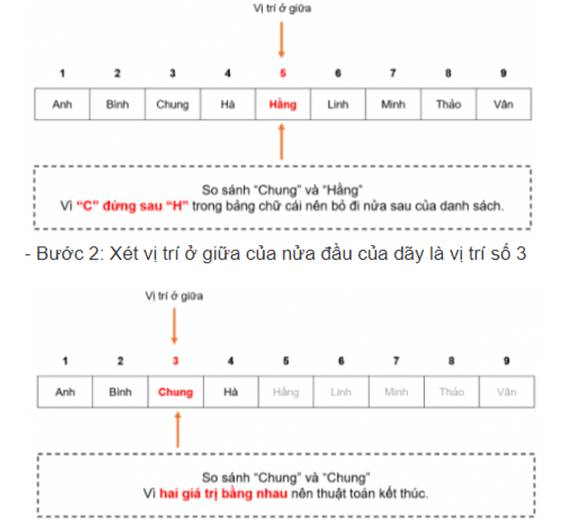
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.
b) Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.
Thuật toán tuần tự
- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.
- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.
- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.

def sequential_search(names, target):
found = []
for name in names:
if name == target:
found.append(name)
return found
# Danh sách tên học sinh trong lớp
class_names = ["An", "Bình", "Cường", "Đạt", "Hoàn", "Minh", "Nam", "Thảo", "Hoàn", "Trung"]
# Tên học sinh cần tìm
target_name = "Hoàn"
# Danh sách tên học sinh trong lớp
class_names = ["An", "Bình", "Cường", "Đạt", "Hoàn", "Minh", "Nam", "Thảo", "Hoàn", "Trung"]
# Tên học sinh cần tìm
target_name = "Hoàn"
# Gọi hàm tìm kiếm tuần tự
found_names = sequential_search(class_names, target_name)
if len(found_names) > 0:
print("Các học sinh có tên là", target_name, "là:", found_names)
else:
print("Không tìm thấy học sinh nào có tên là", target_name)

program bai1;
uses crt;
var i:integer;
s,s1:string;
begin
clrscr;
write('nhap S:');readln(s);
while pos('C',s)<>0 do
begin
insert('LOP11A',s,pos('C',s));
delete(s,pos('C',s),1);
end;
writeln('xau sau khi bien doi la: ',s);
writeln('do dai cua xau tren la: ',length(s));
write('nhap s1:');readln(s1);
if s1[1]=s[1] then writeln('ki tu dau cua hai xau trung nhau')
else writeln('ki tu dau cua hai xau khong trung nhau');
readln;
end.

Tham khảo:
#Trả về chỉ số của x trong arr nếu tồn tại, nếu không có sẽ trả về -1
def binary_search(arr, low, high, x):
#Trường hợp cơ sở
if high >= low:
mid = (high + low) // 2
#Nếu phần tử có tồn tại ở phần giữa của mảng
if arr[mid] == x:
return mid
#Nếu phần tử nhỏ hơn mid, nó sẽ nằm ở phía bên trái của mảng điểm gốc là tử phần tử mid
elif arr[mid] > x:
return binary_search(arr, low, mid - 1, x)
#Nếu không, phần tử sẽ nằm bên phải
else:
return binary_search(arr, mid + 1, high, x)
else:
#Phần tử không tồn tại trong tập hợp
return -1
#Khởi tạo tập hợp
arr = [ 2, 3, 4, 10, 40 ]
x = 10
#Gọi hàm
result = binary_search(arr, 0, len(arr)-1, x)
if result != -1:
print("Phần tử cần tìm có chỉ số là ", str(result))
else:
print("Phần tử cần tìm không có trong mảng.")

Truy cập trang web www.google.com, tai ô tìm kiếm nhập lần lượt các biểu thức tìm kiếm ở trên, quan sát và nhận xét các kết quả nhận được.
Google hỗ trợ các kí hiệu đặc biệt và toán tử nhằm tăng hiệu quả tìm kiếm, mốt số kí hiệu đó như sau (kí hiệu A, B là các từ khoá tìm kiếm):
- “A”: Tìm trang chứa chính xác từ khoá A
- A-B: Tìm trang chưa từ khoá A nhưng không chứa từ khoá B.
- A+B: Tìm trang kết quả chứa cả từ khoá A và B nhưng không cần theo thứ tự. -- A*: Tìm trang chứa từ khoá A và một số từ khác mà Google xem là có liên quan. Ví dụ: Từ khoá “tin học* tìm các trang có chứa từ “tin học ứng dụng”, “tin học văn phòng”.
- AAND B: Tìm trang chứa cả từ khoá A và B.
- AOR B (hoặc A | B): Tìm trang chứa từ khoá A hoặc B. Toán tử này hữu ích khi tìm từ đồng nghĩa hoặc một từ có nhiều cách viết.
- A + filetype (loại tệp): Tìm thông tin chính xác theo loại tệp như “txt”, “doc”, “pdf”,.... Sử dụng từ khoá này thuận lợi trong tìm kiếm tài liệu, sách điện tử.

a)
import time
def linear_search(arr, x):
"""
Tìm kiếm tuyến tính trong dãy arr để tìm giá trị x.
Trả về vị trí của x trong dãy nếu x được tìm thấy, -1 nếu không tìm thấy.
"""
n = len(arr)
for i in range(n):
if arr[i] == x:
return i
return -1
# Dãy số A
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 11]
# Phần tử cần tìm kiếm
C = 9
# Bắt đầu đo thời gian
start_time = time.perf_counter()
# Tìm kiếm phần tử C trong dãy A
result = linear_search(A, C)
# Kết thúc đo thời gian
end_time = time.perf_counter()
if result != -1:
print(f"Phần tử {C} được tìm thấy tại vị trí {result} trong dãy A.")
else:
print(f"Phần tử {C} không có trong dãy A.")
print(f"Thời gian thực hiện thuật toán: {end_time - start_time} giây.")
b)
import time
def binary_search(arr, x):
"""
Tìm kiếm nhị phân trong dãy arr để tìm giá trị x.
Trả về vị trí của x trong dãy nếu x được tìm thấy, -1 nếu không tìm thấy.
"""
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == x:
return mid
elif arr[mid] < x:
left = mid + 1
else:
right = mid - 1
return -1
# Dãy số A đã được sắp xếp
A = [0, 1, 3, 5, 7, 9, 10, 11, 13, 16]
# Phần tử cần tìm kiếm
C = 9
# Bắt đầu đo thời gian
start_time = time.perf_counter()
# Tìm kiếm phần tử C trong dãy A bằng thuật toán tìm kiếm nhị phân
result = binary_search(A, C)
# Kết thúc đo thời gian
end_time = time.perf_counter()
if result != -1:
print(f"Phần tử {C} được tìm thấy tại vị trí {result} trong dãy A.")
else:
print(f"Phần tử {C} không có trong dãy A.")
print(f"Thời gian thực hiện thuật toán: {end_time - start_time} giây.")
-Thời gian thực hiện ở câu a là 8.99999,thời gian thực hiện ở câu b là 6,49999 giây.

Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.
Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.
Tham khảo:
a. Viết chương trình phython thực hiện tìm kiếm tuần tự
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# Driver Code
arr = [ 2, 3, 4, 10, 40 ];
x = 10;
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result);
b. Viết phiên bản tìm kiếm tuần tự thứ hai, dùng vòng lặp for thay cho vòng lặp while (hoặc ngược lại).
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# Driver Code
arr = [ 2, 3, 4, 10, 40 ];
x = 10;
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result);
c. Viết phiên bản tìm kiếm tuần tự có thêm hai tham số đầu vào lo và hi tương tự như của hàm index. So sánh kết quả với phương thức index của phython.
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# Driver Code
arr = [ 2, 3, 4, 10, 40 ];
x = 10;
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result);