K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8 2024
A = - 3\(x\).(\(x-5\)) + 3(\(x^2\) - 4\(x\)) - 3\(x\) - 10
A = - 3\(x^2\) + 15\(x\) + 3\(x^2\) - 12\(x\) - 3\(x\) - 10
A = (- 3\(x^2\) + 3\(x^2\)) + (15\(x\) - 12\(x\) - 3\(x\)) - 10
A = 0 + (3\(x-3x\)) - 10
A = 0 - 10
A = - 10
T
0
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
30 tháng 4 2023
\(a\\ -5x^2+3x.\left(x+2\right)=-5x^2+3x^2+6x=-2x^2+6x\\ b\\ -2x.\left(1-x^2\right)-2x^3=-2x+2x^3-2x^3=-2x\\ c\\ 4x.\left(x-1\right)-4.\left(x^2+2x-1\right)\\ =4x^2-4x-4x^2-8x+4=-12x+4\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
30 tháng 4 2023
\(d\\ 6x^3-2x^2.\left(-x^2-3x\right)=6x^3+2x^4+6x^3=2x^4+12x^3\\ e\\ 3x.\left(x-1\right)-\left(1+2x\right).5x\\ =3x^2-3x-5x-10x^2=-7x^2-8x\\ f\\ -5x^2-\left(x-6\right).\left(-2x^2\right)=-5x^2+2x^3-12x^2=2x^3-17x^2\)
20 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
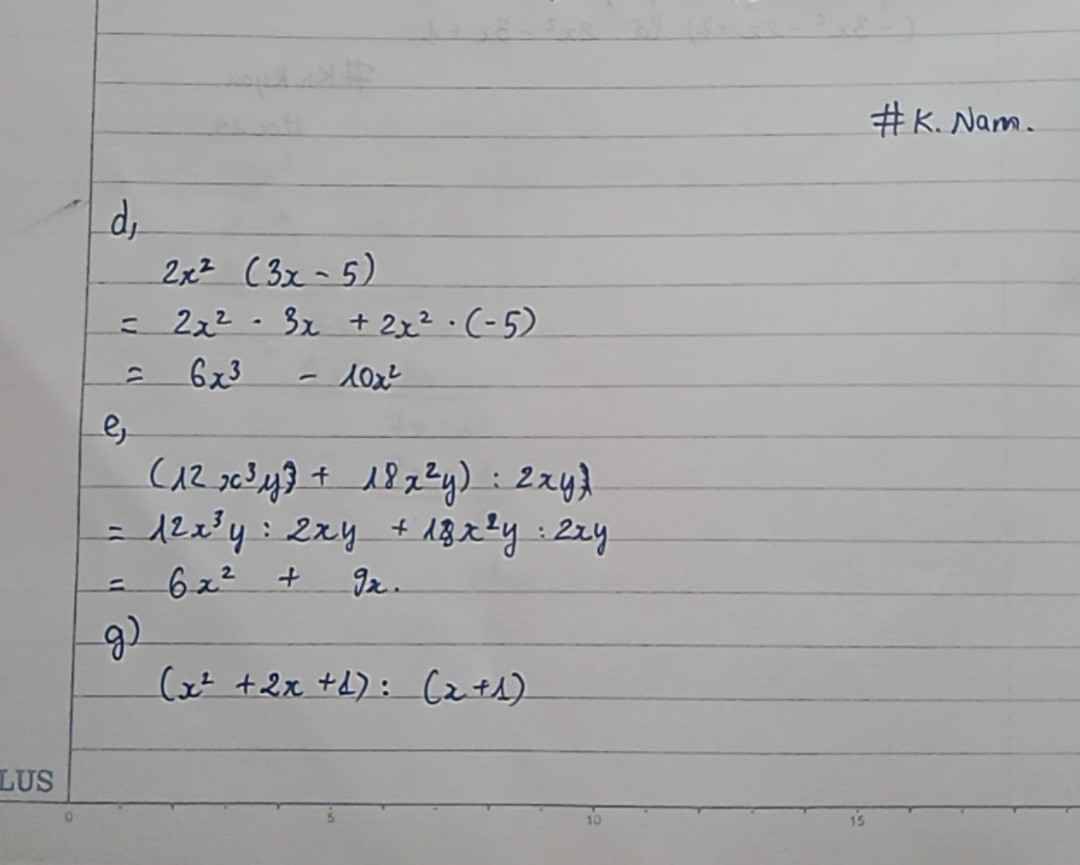
*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.
HQ
4
10 tháng 9 2017
Tham khảo nhé :
\(\left|x-2\right|-3x\left|+\right|x-1\left|x-3\right|=0\)
\(\Leftrightarrow\left|x-2\right|-3=0\)hoặc \(5+\left|x\right|=0\)
Xét \(\left|x-2\right|-3=0\Leftrightarrow\left|x-2\right|=3\)
\(\Rightarrow x-2=\pm3\)
Với: \(x-2=3\Rightarrow x=5\)
Với: \(x-2=-3\Rightarrow x=-1\)
Vậy:..
H
27 tháng 4 2023
\(a,\left(4x+1\right)\left(x-3\right)-\left(x-7\right)\left(4x-1\right)=15\\ \Leftrightarrow4x^2+x-12x-3-\left(4x^2-28x-x+7\right)-15=0\\ \Leftrightarrow4x^2-11x-3-4x^2+29x-7-15=0\\ \Leftrightarrow18x=25\\ \Leftrightarrow x=\dfrac{25}{18}\)
Vậy \(x=\dfrac{25}{18}\)
\(b,\left(x+1\right)\left(x^2-x+1\right)-x\left(x^2-3\right)=4\\ \Leftrightarrow x^3+1-x^3+3x-4=0\\ \Leftrightarrow3x-3=0\\ \Leftrightarrow x=1\)
Vậy \(x=1\)
\(c,\left(x-3\right)\left(x^2+3x+9\right)+x\left(5-x^2\right)-6x=0\\ \Leftrightarrow x^3-27+5x-x^3-6x=0\\ \Leftrightarrow-x-27=0\\ \Leftrightarrow x=-27\)
Vậy \(x=-27\)
\(d,\left(5x-1\right)\left(5x+1\right)=25x^2-7x+15\\ \Leftrightarrow25x^2-1-25x^2+7x-15=0\\ \Leftrightarrow7x-16=0\\ \Leftrightarrow x=\dfrac{16}{7}\)
Vậy \(x=\dfrac{16}{7}\)
TC
2 tháng 3 2023
a) `3x+5 =0`
`3x=-5`
`x=-5/3`
`b) -4x+8=0`
`-4x =-8`
`x=2`
`c) 3x -6=0`
`3x=6`
`x=2`
`d)x^2 +x =0`
`x(x+1) =0`
`=>[(x=0),(x=-1):}`
`e) x^2 -4 =0`
`x^2 =4`
`=> x = +-2`
`f) x^3 -27 =0`
`x^3 =27`
`=> x=3`
`g) 3x^2 +4 =0`
`3x^2 =-4`
`x^2 =-4/3(vô-lí)`
=> Đa thức ko có nghiệm
h) `x^3 -4x =0`
`x(x^2 -4) =0`
`=>[(x=0),(x^2=4 => x=+-2):}`
i) `2x^3 -32x =0`
`2x(x^2 -16)=0`
`=>[(2x=0),(x^2=16):}`
`=>[(x=0),(x=+-4):}`
HH
29 tháng 6 2018
Giải:
\(E=x^2-3x-15\)
\(\Leftrightarrow E=x^2-2.x.\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2-\dfrac{69}{4}\)
\(\Leftrightarrow E=\left(x-\dfrac{3}{2}\right)^2-\dfrac{69}{4}\ge-\dfrac{69}{4};\forall x\)
\(\Leftrightarrow E_{Min}=-\dfrac{69}{4}\)
\("="\Leftrightarrow x-\dfrac{3}{2}=0\Leftrightarrow x=\dfrac{3}{2}\)
Vậy ...
\(E=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{69}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2-\dfrac{69}{4}>=-\dfrac{69}{4}\)
Dấu '=' xảy ra khi x=3/2