Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M=\left(m;m+5\right)\left(m\in\right)R\) là điểm cần tìm.
\(\Rightarrow IM=\sqrt{2m^2+32}\)
Ta có: \(cos\left(AM;IM\right)=cos45^o\)
\(\Leftrightarrow\dfrac{R}{IM}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{2m^2+32}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\) vô nghiệm
Vậy không tồn tại điểm M thỏa mãn yêu cầu bài toán.

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
Tam giác PAB đều \(\Leftrightarrow\widehat{APB}=60^0\Rightarrow\widehat{API}=30^0\)
\(\Rightarrow IP=\frac{IA}{sin30^0}=2IA=2R=6\)
\(\Rightarrow P\) thuộc đường tròn (C') tâm I bán kính 6
Để có duy nhất điểm P \(\Leftrightarrow\) d tiếp xúc (C')
\(\Leftrightarrow d\left(I;d\right)=6\Leftrightarrow\frac{\left|3.1-4\left(-2\right)+m\right|}{\sqrt{3^2+\left(-4\right)^2}}=6\)
\(\Leftrightarrow\left|m+11\right|=30\Rightarrow\left[{}\begin{matrix}m=19\\m=-41\end{matrix}\right.\)

Thay \(y=0\) vào pt (C) ta được: \(\left(x+2\right)^2=-11\) (vô nghiệm)
\(\Rightarrow\)Ox không cắt (C)
Gọi \(I\left(-2;4\right)\) là tâm đường tròn và \(M\left(a;0\right)\)
Theo tính chất tiếp tuyến ta có \(IA\perp MA\Rightarrow\Delta IMA\) vuông tại A
\(\Rightarrow MA=\sqrt{IM^2-IA^2}=\sqrt{IM^2-R^2}\)
\(\Rightarrow MA\) ngắn nhất khi \(IM\) nhỏ nhất \(\Rightarrow M\) là hình chiếu vuông góc của I lên Ox \(\Rightarrow M\left(-2;0\right)\)

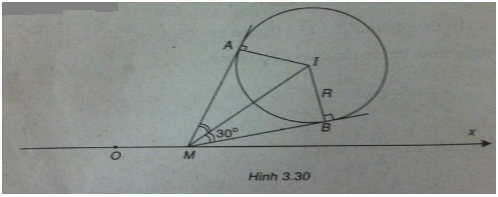
Đường tròn (C) có tâm I (3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\(\Leftrightarrow {x^2} - 6x + 2 = 0\)
\(\Leftrightarrow x = 3 \pm \sqrt 7\)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)

Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=1\)
Gọi \(M\left(m;m+3\right)\) \(\Rightarrow\) đường tròn (C') tâm M có bán kính \(R'=2\)
Do (C) và (C') tiếp xúc ngoài
\(\Rightarrow IM=R+R'=3\)
\(\overrightarrow{IM}=\left(m-1;m+2\right)\Rightarrow\left(m-1\right)^2+\left(m+2\right)^2=9\)
\(\Leftrightarrow m^2+m-2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(1;4\right)\\M\left(-2;1\right)\end{matrix}\right.\)
Đường tròn (C) tâm \(I\left(1;3\right)\) bán kính \(R=\sqrt{10}\)
Gọi 2 tiếp điểm là A và B \(\Rightarrow\) tứ giác IAMB là hình chữ nhật (có 3 góc vuông)
Mà \(IA=IB=R\Rightarrow IAMB\) là hình vuông (hcn có 2 cạnh kề bằng nhau)
\(\Rightarrow IM=IA\sqrt{2}=R\sqrt{2}=2\sqrt{5}\)
Gọi \(M\left(3;m\right)\Rightarrow\overrightarrow{IM}=\left(2;m-3\right)\)
\(\Rightarrow IM=\sqrt{4+\left(m-3\right)^2}=2\sqrt{5}\)
\(\Leftrightarrow\left(m-3\right)^2=16\Rightarrow\left[{}\begin{matrix}m=-1\\m=7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(3;-1\right)\\M\left(3;7\right)\end{matrix}\right.\)