Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

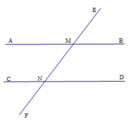
Ta có: AME ^ + EMB ^ = 180 ∘ (hai góc kề bù)
Mà AME ^ = 3 EMB ^
⇒ 3 EMB ^ + EMB ^ = 180 ∘
⇒ 4 EMB ^ = 180 ∘
⇒ EMB ^ = 180 ∘ : 4
⇒ EMB ^ = 45 ∘ (1)
Ta có: AME ^ + EMB ^ + MND ^ = 225 ∘
⇒ 180 ∘ + MND ^ = 225 ∘
⇒ MND ^ = 225 ∘ − 180 ∘
⇒ MND ^ = 45 ∘ (2)
Từ (1) và (2) suy ra EMB ^ = MND ^ mà hai góc này ở vị trí đồng vị
AB // CD

A B C D E F M N
\(\widehat{AMB}=\widehat{AME}+\widehat{EMB}=3\widehat{EMB}+\widehat{EMB}=4\widehat{EMB}=180^o\)
\(\Rightarrow\widehat{EMB}=180^o:4=45^o\)
Ta có
\(\widehat{AME}+\widehat{EMB}+\widehat{MND}=\widehat{AMB}+\widehat{MND}=225^o\)
\(\Rightarrow180^o+\widehat{MND}=225^o\Rightarrow\widehat{MND}=225^o-180^o=45^o\)
Gọi O là giao của AB và CD xét tg OMN có
\(\widehat{MON}=180^o-\left(\widehat{EMB}+\widehat{MND}\right)=180^o-\left(45^o+45^o\right)=90^o\)
\(\Rightarrow AB\perp CD\)

A B C D M N P Q
- Theo đề bài, ta có : \(APM+MPB+PQD=\)\(216^O\)
Mà \(ABM\)kề bù \(MPB\)\(\Rightarrow APM+MPB=180^O\)
Nên \(PQD=36^O\)\(\left(1\right)\)
- \(APM+MPB=180^O\)
Mà \(APM=4MPB\)
\(\Rightarrow4MPB+MPB=180^O\)
\(\Rightarrow5MPB=180^O\)
\(\Rightarrow MPB=36^O\)\(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow PQD=MPB=36^O\)
Mà 2 góc trên ở vị trí đồng vị \(\Rightarrow AB\)// \(CD\)