Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)

Dựng một tam giác vuông ta có:
a, Độ dài cạnh góc vuông là 3, cạnh huyền là 5, góc đối diện với cạnh góc vuông đó là góc α
b, Độ dài cạnh góc vuông là 4, cạnh huyền là 7,góc giữa cạnh góc vuông và cạnh huyền đó là góc α
c, Độ dài hai cạnh góc vuông là 3 và 2, góc đối diện với cạnh góc vuông độ dài 3 là góc α
d, Độ dài hai cạnh góc vuông là 5 và 6, góc đối diện với cạnh góc vuông độ dài 6 là góc α

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
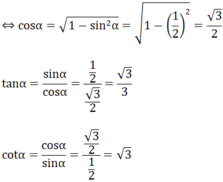

dung may tinh la xong thui ban oi
hoac dua len mang giai
chao <>?

ta có :\(\sin2=\dfrac{\sqrt{3}}{2}\Rightarrow2=60^0\)
\(\cos60^o=\dfrac{1}{2};\tan60^o=\sqrt{3};\cot60^o=\dfrac{1}{\sqrt{3}}\)

Ta có:
\(cot\alpha\cdot tan\alpha=1\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}\)
\(\Rightarrow cota=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Mà:
\(cot^2\alpha+1=\dfrac{1}{sin^2\alpha}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{cot^2\alpha+1}}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{\left(\dfrac{4}{3}\right)^2+1}}=\dfrac{3}{5}\)
Lại có:
\(cos^2\alpha+sin^2\alpha=1\)
\(\Rightarrow cos\alpha=\sqrt{1-sin^2a}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
\(tan\alpha=\dfrac{3}{4}\\ \Rightarrow cot\alpha=1:\dfrac{3}{4}=\dfrac{4}{3}\)
Có:
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\\ \Rightarrow sin\alpha=\sqrt{1:\left(1+\left(\dfrac{4}{3}\right)^2\right)}=\dfrac{3}{5}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
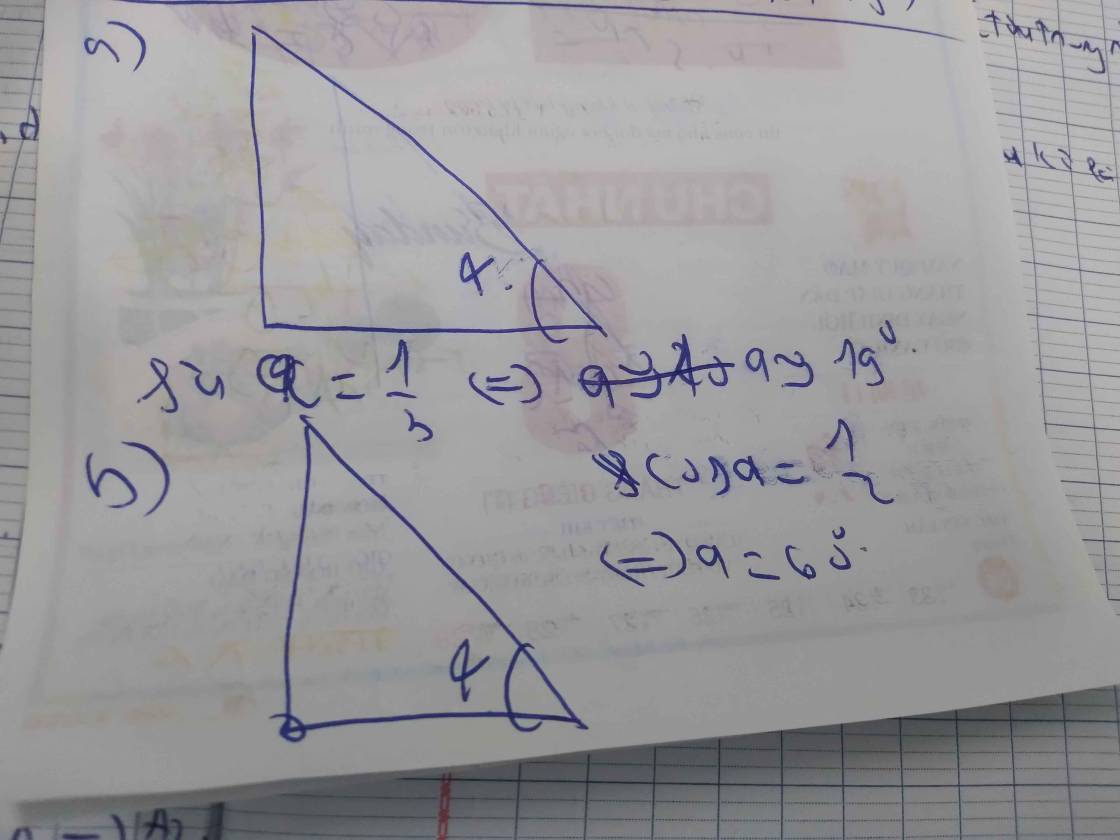
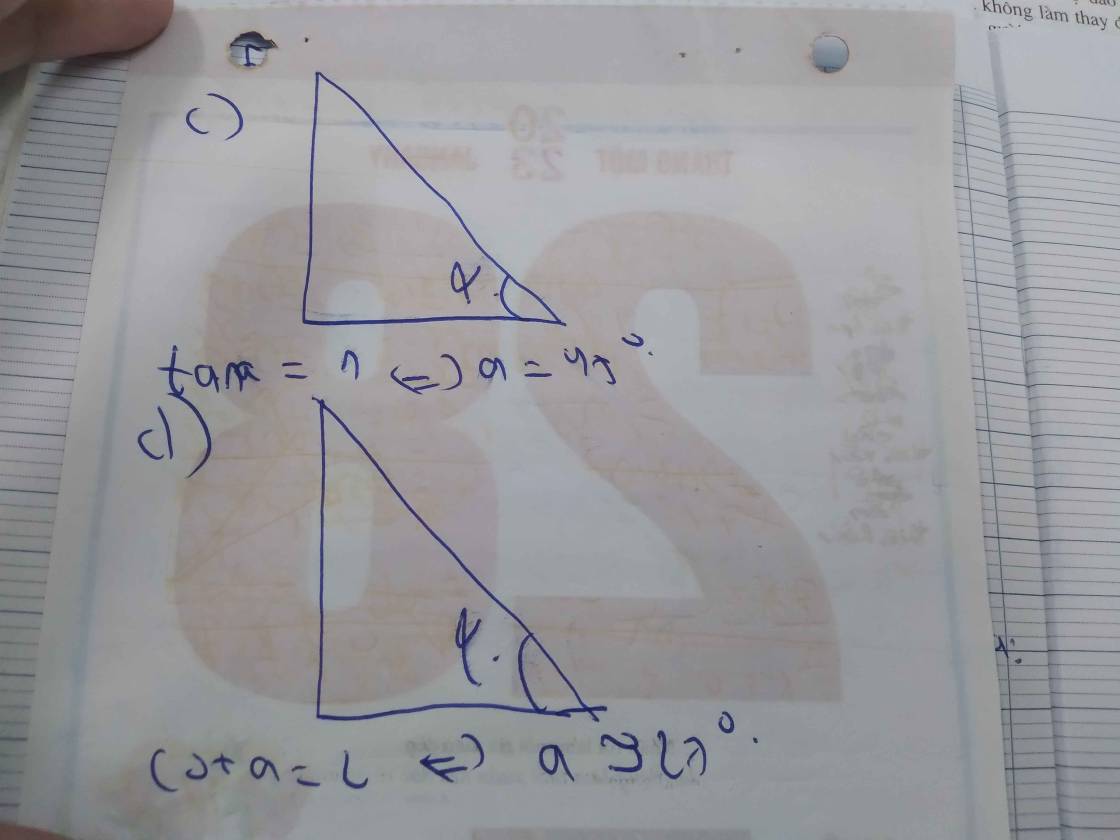
a ) \(\tan\alpha=\dfrac{3}{4}\Rightarrow\alpha=36^052'11,63"\)
b ) \(\sin\alpha=0,5\Rightarrow\alpha=\dfrac{1}{2}\)
c ) \(\cos\alpha=\dfrac{2}{5}\Rightarrow\alpha=66^025'18,56"\)
d ) \(\cot\alpha=3\Rightarrow\alpha=18^026'5,82"\)
câu b bác lm sai rùi