Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .

Gọi \(A_i\) là biến cố cầu thủ sút vào vị trí \(i\) và \(B_i\) là biến cố thủ môn bay người tới vị trí \(i\)
Do 4 vị trí như nhau nên \(P\left(A_i\right)=P\left(B_i\right)=\dfrac{1}{4}\) với mọi i từ 1 tới 4
Xác suất cầu thủ ko sút vào là:
\(P=P\left(A_1\right).P\left(B_1\right)+P\left(A_2\right).P\left(B_2\right)+\dfrac{1}{2}P\left(A_3\right).P\left(B_3\right)+\dfrac{1}{2}P\left(A_4\right).P\left(B_4\right)\)
\(=\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{2}.\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{2}\dfrac{1}{4}.\dfrac{1}{4}=\dfrac{3}{16}\)

Những trận đấu giữa Real Madrid và Barcelona luôn rất rất căng thẳng và đỉnh điểm chính là trong giai đoạn 1953-1966 và 2010-2013

Đáp án A
Số vòng đấu là ![]() vòng đấu (gồm cả lượt đi và về)
vòng đấu (gồm cả lượt đi và về)
Mỗi vòng đấu có 7 trận đấu
Do đó có tất cả ![]() trận đấu
trận đấu

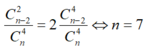
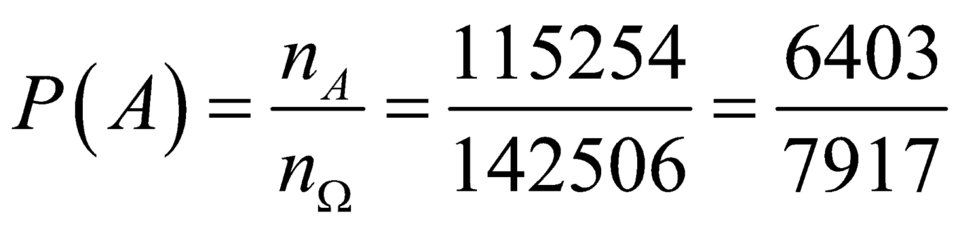
Hmm, đề bài vẫn chưa rõ ràng lắm, trong đội hình 442 kia, vị trí của 4 cầu thủ trong hàng hậu vệ là như nhau, hay phân biệt rõ ràng hậu vệ cánh trái, hậu vệ cánh phải và 2 trung vệ? Tương tự với hàng tiền vệ, có tiền vệ trụ, tiền vệ kiến thiết, tiền vệ công, hộ công v...v...
Cứ coi như các cầu thủ ở 3 tuyến là như nhau
Không gian mẫu: \(C_3^1.C_8^4.C_6^4.C_6^2\)
Số cách chọn đội hình thỏa mãn yêu cầu: \(C_7^3.C_4^2.C_5^1\)
Xác suất: \(P=\frac{1}{45}\)
Hay lắm,
thanks