Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

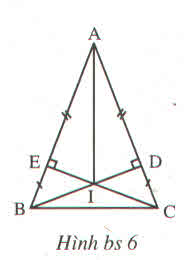
Xét tam giác AIE và tam giác AID có:
AE = AD (theo đề bài)
góc AEI = góc ADI = \(90^0\)
AI là cạng chung
Do đó tam giác AIE = tam giác AID (cạnh huyền và cạnh góc vuông) úuy ra góc A1 = A2 (2 góc tương ứng) (1)
Suy ra: EI = DI (2 cạnh tương ứng)(*)
Xét tam giác IEB và tam giác IDC có:
EI = DI (*)
góc IEB = góc IDC = \(90^0\)
EB = DC ( theo đề bài)
Do đó tam giác IEB = tam giác IDC (2 cạnh góc vuông)
Có BE + AE = AB
CD + AD = AC
mà: AE = AD, EB = DC (theo đề bài)
Suy ra: AB = AC (2)
Xét tam giác AIB và tam giác AIC có:
AB = AC (2)
góc A1 = góc A2 (1)
AI là cạnh chung
Do đó: tam giác AIB = tam giác AIC (c.g.c)
Xét tam giác ECB và tam giác DBC có:
EB = DC ( theo đề bài)
góc CEB = góc BDC = \(90^0\)
Do đó: tam giác ECB = tam giác DBC (cạnh huyền và cạnh góc vuông)
Suy ra: EC = BD (2 cạnh tương ứng) (3)
Xét tam giác AEC và tam giác ADB có:
AE = AD (theo đề bài)
góc AEC = góc ADB = \(90^0\)
EC = BD (3)
Do đó: tam giác AEC = tam giác ADB ( 2 cạnh góc vuông)
Vậy đáp án đúng là: (D) 5 cặp tam giác bằng nhau trong hình bs 6

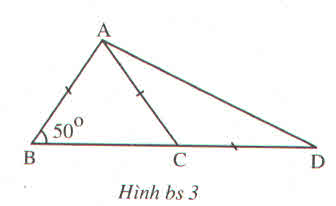
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)

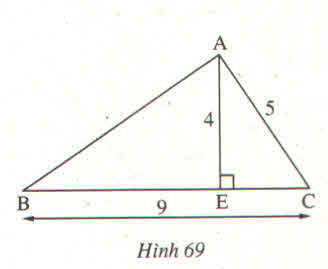
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)






Đáp án đúng là : (D) 12
D:12